机器学习笔记-VC Dimension, Part III
笔记整理自台大林轩田老师的开放课程-机器学习基石,笔记中所有图片来自于课堂讲义。
上一篇讲到了VC Dimension以及VC Bound。VC Bound所描述的是在给定数据量N以及给定的Hypothesis Set的条件下,遇到坏事情的概率的上界,即$E_{in}$与$E_{out}$差很远的概率,最多是多少。VC Bound用公式表示就是:
其中$m_{\mathcal{H}}(N)$为Hypothesis Set的成长函数,有:
因为寻找所有Hypothesis Set的成长函数是困难的,因此我们再利用$N^{d_{vc}}$来bound住所有VC Dimension为$d_{vc}$的Hypothesis Set的成长函数。所以对于任意一个从$\mathcal{H}$中的$g$来说,有:
因此说想让机器真正学到东西,并且学得好,有三个条件:
- $\mathcal{H}$的$d_{vc}$是有限的,这样VC Bound才存在。(good $\mathcal{H}$)
- $N$足够大(对于特定的$d_{vc}而言$),这样才能保证上面不等式的bound不会太大。(good $\mathcal{D}$)
- 算法$\mathcal{A}$有办法在$\mathcal{H}$中顺利地挑选一个使得$E_{in}$最小的方程$g$。(good $\mathcal{A}$)
为什么要费那么大的力气来讲这个VC Bound和VC Dimension呢?因为对于初学者来说,最常犯的错误就是只考虑到了第3点,而忽略掉了前两点,往往能在training set上得到极好的表现,但是在test set中表现却很烂。关于算法$\mathcal{A}$的部分会在后续的笔记当中整理,目前我们只关心前面两点。
几种Hypothesis Set的VC Dimension
对于以下几个$\mathcal{H}$,由于之前我们已经知道了他们的成长函数(见机器学习笔记-VC Dimension, Part I),因此可以根据$m_{\mathcal{H}}(N)\leq N^{d_{vc}}$,直接得到他们的VC Dimension:
- positive rays: $m_{\mathcal{H}}(N)=N+1$,看N的最高次项的次数,知道$d_{vc}=1$
- positive intervals: $m_{\mathcal{H}}(N)=\frac{1}{2}N^2+\frac{1}{2}N+1$,$d_{vc}=2$
- convex sets: $m_{\mathcal{H}}(N)=2^N$,$d_{vc}=\infty$
- 2D Perceptrons: $m_{\mathcal{H}}(N)\leq N^3\;for\;N\geq 2$,所以$d_{vc}=3$
由于convex sets的$d_{vc}=\infty$,不满足上面所说的第1个条件,因此不能用convex sets这个$\mathcal{H}$来学习。
但这里要回归本意,通过成长函数来求得$d_{vc}$没有太大的意义,引入$d_{vc}$很大的一部分原因是,我们想要得到某个Hypothesis Set的成长函数是困难的,希望用$N^{d_{vc}}$来bound住对应的$m_{\mathcal{H}}(N)$。对于陌生的$\mathcal{H}$,如何求解它的$d_{vc}$呢?
某个$\mathcal{H}$的VC Dimension - 从”shatter”的角度
Homework当中的某题,求解简化版决策树的VC Dimension:
Consider the simplified decision trees hypothesis set on $\mathbb{R}^d$, which is given by
That is, each hypothesis makes a prediction by first using the $d$ thresholds $t_i$ to locate $x$ to be within one of the $2^d$ hyper-rectangular regions, and looking up $S$ to decide whether the region should be +1 or −1. What is the VC-dimension of the simplified decision trees hypothesis set?
如何去理解题意呢?用一个2维的图来帮助理解:
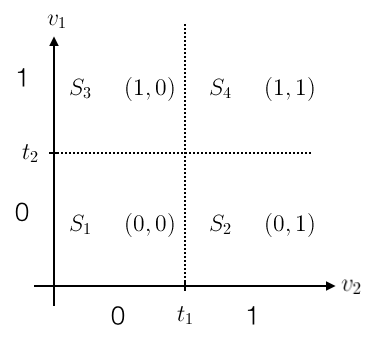
首先把二维实数空间$\mathbb{R}^2$中的向量$x$,通过各个维度上的阈值$t_i$,转换到${{0,1}}^2$空间下的一个点$v$,规则为$v_i=[x_i\gt t_i]$。譬如对于$t=[5,10]$,$x=[6,8]$可以转换为新的空间下的$[1,0]$。这样一来,原来的$\mathbb{R}^2$空间就可以被划分为4个区块$S_1$~$S_4$(hyper-rectangular regions)。$\mathcal{H}$中每一个方程$h$代表着一种对这4块区域是”圈圈“还是”叉叉“的决策(decision),并且这4块区域的决策是互相独立的,$S_1$的决策是”圈圈“还是”叉叉“和$S_2,S_3,S_4$都没有关系。
由于这4块区域的决策是互相独立的,那么它最多最多能shatter掉多少个点呢?4个,(当这4个点分别属于这4块区域的时候),即这4块hyper-rectangular regions所代表的类别可以是(o,o,o,o)、(o,o,o,x)、(o,o,x,o)、…、(x,x,x,x),共16种可能,因此它能够shatter掉4个点。
由上面2维的例子我们可以看出,simplified decision trees的VC Dimension,等于hyper-rectangular regions的个数。$d$维空间$\mathbb{R}^d$可以用$d$条直线切分出$2^d$个互相独立的hyper-rectangular regions,即最多最多可以shatter掉$2^d$个点,因此simplified decision trees的$d_{vc}=2^d$。
我们再来回顾一下Positive Intervals:

也可以按照上面的方法去理解,Positive Intervals有两个thresholds,把直线切分为3块空间。但这3块空间并不是相互独立,中间的部分永远是+1,左右两边永远是-1,所以还要具体看它能够shatter掉多少个点,这里最多最多只能shatter掉2个点,它的$d_{vc}=2$。
某个$\mathcal{H}$的VC Dimension - 从”自由度”的角度
对于$d_{vc}$较小的$\mathcal{H}$,可以从它最多能够shatter的点的数量,得到$d_{vc}$,但对于一些较为复杂的模型,寻找能够shatter掉的点的数量,就不太容易了。此时我们可以通过模型的自由度,来近似的得到模型的$d_{vc}$。
维基百科上有不止一个关于自由度的定义,每种定义站在的角度不同。在这里,我们定义自由度是,模型当中可以自由变动的参数的个数,即我们的机器需要通过学习来决定模型参数的个数。
譬如:
- Positive Rays,需要确定1个threshold,这个threshold就是机器需要根据$\mathcal{D}$来确定的一个参数,则Positive Rays中自由的参数个数为1,
- Positive Intervals,需要确定左右2个thresholds,则可以由机器自由决定的参数的个数为2,$d_{vc}=2$
- d-D Perceptrons,$d$维的感知机,可以由机器通过学习自由决定的参数的个数为$d+1$(别忘了还有个$w_0$),$d_{vc}=d+1$
多个$\mathcal{H}$的并集的VC Dimension
Homework当中某题,求$K$个Hypothesis Set的并集$d_{vc}(\cup_{k=1}^{K}\mathcal{H}_k)$的VC Dimension的上下界。下界比较好判断,是$max\{d_{vc}(\mathcal{H}_k)\}_{k=1}^K$,即所有的$\mathcal{H}$都包含于$d_{vc}$最大的那个$\mathcal{H}$当中的时候。上界则出现在各个$\mathcal{H}$互相都没有交集的时候,我们不妨先来看看$K=2$的情况:
求$d_{vc}(\mathcal{H}_1\cup \mathcal{H}_2)$的上界,已知$d_{vc}(\mathcal{H}_1)=d_1$,$d_{vc}(\mathcal{H}_2)=d_2$。
从成长函数上看,有 $m_{\mathcal{H}_1\cup \mathcal{H}_2}(N) \leq m_{\mathcal{H}_1}(N) + m_ {\mathcal{H}_2}(N)$,把成长函数展开,有
用$\binom{N}{i}=\binom{N}{N-i}$替换RHS,有
我们可以尝试寻找下上面这个成长函数有可能的最大的break point,让$N$不断增大,直到出现$m_{\mathcal{H}_1\cup \mathcal{H}_2}(N)\lt 2^N$的时候,这个$N$就是break point。那么$N$要多大才够呢?
$N=d_1$够大吗?不够,因为:
$N=d_1+d_2+1$够大吗?还是不够,因为:
$N=d_1+d_2+2$够大吗?够大了,因为:
所以$m_{\mathcal{H}_1\cup \mathcal{H}_2}(N)$的break point最大可以是$d_1+d_2+2$,此时$d_{vc}(\mathcal{H}_1\cup \mathcal{H}_2)=d_1+d_2+1$。
因此两个$\mathcal{H}$的并集的VC Dimension的上界为$d_{vc}(\mathcal{H}_1)+d_{vc}(\mathcal{H}_2)+1$。利用此方法,就很容易可以推出$K$个$\mathcal{H}$的并集的情况。
简单 v.s 复杂
机器学习笔记-VC Dimension, Part I一开始就提到,learning的问题应该关注的两个最重要的问题是:1.能不能使$E_{in}$与$E_{out}$很接近,2.能不能使$E_{in}$足够小。
- 对于相同的$\mathcal{D}$而言,$d_{vc}$小的模型,其VC Bound比较小,比较容易保证$E_{in}$与$E_{out}$很接近,但较难做到小的$E_{in}$,试想,对于2D Perceptron,如果规定它一定要过原点($d_{vc}=2$),则它就比没有规定要过原点($d_{vc}=3$)的直线更难实现小的$E_{in}$,因为可选的方程更少。2维平面的直线,就比双曲线($d_{vc}=6$),更难实现小的$E_{in}$。
- 对于相同的$\mathcal{D}$而言,$d_{vc}$大的模型,比较容易实现小的$E_{in}$,但是其VC Bound就会很大,很难保证模型对$\mathcal{D}$之外的世界也能有同样强的预测能力。
令之前得到的VC Bound为$\delta$,坏事情$[|E_{in}(g)-E_{out}(g)|\gt \epsilon]$发生的概率小于$\delta$,则好事情$[|E_{in}(g)-E_{out}(g)|\leq \epsilon]$发生的概率就大于$1-\delta$,这个$1-\delta$在统计学中又被称为置信度,或信心水准。
因此$E_{in}$、$E_{out}$又有下面的关系:
令$\Omega (N,\mathcal{H},\delta)=\sqrt{…}$,即上式的根号项为来自模型复杂度的,模型越复杂,$E_{in}$与$E_{out}$离得越远。
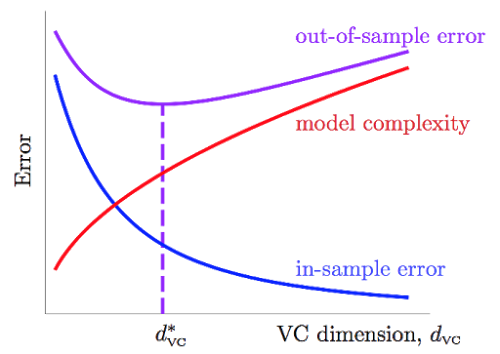
随着$d_{vc}$的上升,$E_{in}$不断降低,而$\Omega$项不断上升,他们的上升与下降的速度在每个阶段都是不同的,因此我们能够寻找一个二者兼顾的,比较合适的$d_{vc}^{*}$,用来决定应该使用多复杂的模型。
反过来,如果我们需要使用$d_{vc}=3$这种复杂程度的模型,并且想保证$\epsilon = 0.1$,置信度$1-\delta =90\%$,我们也可以通过VC Bound来求得大致需要的数据量$N$。通过简单的计算可以得到理论上,我们需要$N\approx 10,000d_{vc}$笔数据,但VC Bound事实上是一个极为宽松的bound,因为它对于任何演算法$\mathcal{A}$,任何分布的数据,任何目标函数$f$都成立,所以经验上,常常认为$N\approx 10d_{vc}$就可以有不错的结果。