Perceptron 是什么？

---

  Perceptron - 感知机，它能够根据每笔资料的特征，把资料判断为不同的类别。令$h(x)$是一个perceptron，你给我一个$x$($x$是一个特征向量)，把$x$输入$h(x)$，它就会输出这个$x$的类别，譬如在信用违约风险预测当中，输出就可能是这个人会违约，或者不会违约。本质上讲，perceptron是一种二元线性分类器，它通过对特征向量的加权求和，并把这个”和”与事先设定的门槛值(threshold)做比较，高于门槛值的输出1，低于门槛值的输出-1。

$$f(x)= \left\{ \begin{matrix} 1 & if\ w^T\cdot x > threshold\\ -1 & else \end{matrix}\right.$$

  更加紧凑一些，我们可以把它写成
$$
h(x) = sign(\sum _{i=1}^{d}w_ix_i+b)
$$
  其中$d$表示维度数，$x$是$d$维空间中的一个点, $x=(x_1,x_2,…,x_d)$; $sign()$输出运算结果的符号，大于0的输出+1，其余输出-1。

  细心一点可以看出，其实$\sum _{i=1}^{d}w_ix_i+b =0$在1维空间中代表一个点，在2维空间中代表一条直线，在3维空间中代表一个平面。

  以2维空间为例:

  对于所有满足$\sum_{i=1}^{d}w_ix_i+b<0$的$x$，将落在直线一边的区域中(下图中的蓝色).

  对于所有满足$\sum _{i=1}^{d}w_ix_i+b > 0$的$x$，将落在直线的另一边(下图中的红色)。

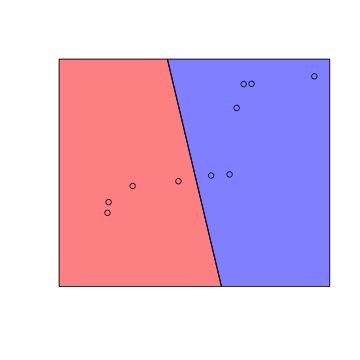
      图1 在2维空间中perceptron是一条直线

  为了方便后面计算，我们常常衍生出一个维度出来，使得$b=w_0x_0,x_0$这个维度恒等于1。则perceptron可以用矩阵的形式表示出来:

$$h(x)=sign(\sum _{i=0}^{d}w_ix_i)=w^Tx$$

  注意: 这里要搞清楚下标的含义，上文中的$x_i$、$w_i$指$x$向量、$w$向量的第$i$个维度。因为后文都是用矩阵乘法，因此下标不再表示维度，譬如$x_n$表示某笔资料，它是一个向量，而$w_t$指第$t$次更新之后的$w$，它也是一个向量。

Perceptron Learning在做什么？

---

  Perceptron Learning Algorithm的目的是要找到一个perceptron，能把正确地把不同类别的点区分开来。
  在二维平面上，任何找一条直线都可以用来做perceptron，只不过有些perceptron分类能力比较好(分错的少)，有些perceptron分类能力比较差(分错的多)。

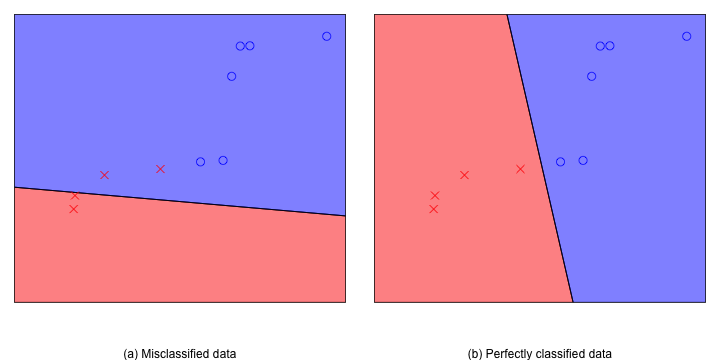
        图2 2维空间中的两个不同的perceptron

  上图中是二维平面上的两个perceptron，图中圈圈代表+1的点，叉叉代表-1的点。左边的perceptron把两个叉叉错分到圈圈当中，而右边的则很完美地把圈圈和叉叉区分开来。在二维平面中存在无数个可能的perceptron，而perceptron learning的目的是找到一个好的perceptron。

  假设给我们的数据是“线性可分”的，即至少存在一个perceptron，它很厉害，可以做到百分百的正确率(如图2-b)，对于任意的$(y_n,x_n)$，有$h(x_n)=y_n$。我们把这个完美的perceptron记为

$$h(x)=sign(w_f^Tx)$$

  则Perceptron Learning要做的是，在“线性可分”的前提下，由一个初始的Perceptron $h(x)$开始，通过不断的learning，不断的调整$h(x)$的参数$w$，使他最终成为一个完美的perceptron。

Perceptron Learning Algorithm (PLA) - “知错就改”演算法

---

  前面说到Perceptron Learning的目的，那么既然要learning就一定有一个learning的方法(譬如随机猜就是一种方法，但它不一定是个好方法)，这个方法能够指导我们该如何去慢慢调整$w$，使$h(x)$越来越接近我们心目中完美的perceptron $sign(w_f^Tx)$。

  PLA的方法如下：

  For t = 0,1,…

1. 找到$w_t$产生的一个错误点

   $sign(w_t^Tx_{n(t)}) \neq y_{n(t)}$

   (注意这里x的下标不是值维度，而是数据点的编号。$y_{n(t)}$指第t次更新后的一个分类错误点)

2. 用下面的方法更正这个错误:

   $w_{t+1} \leftarrow w_t + y_{n(t)}x_{n(t)}$

  …直到找不到错误点，返回最后一次迭代的$w$

  以下用图片展示迭代的过程，图片截至台湾大学林轩田老师Machine Learning Foundation的讲义

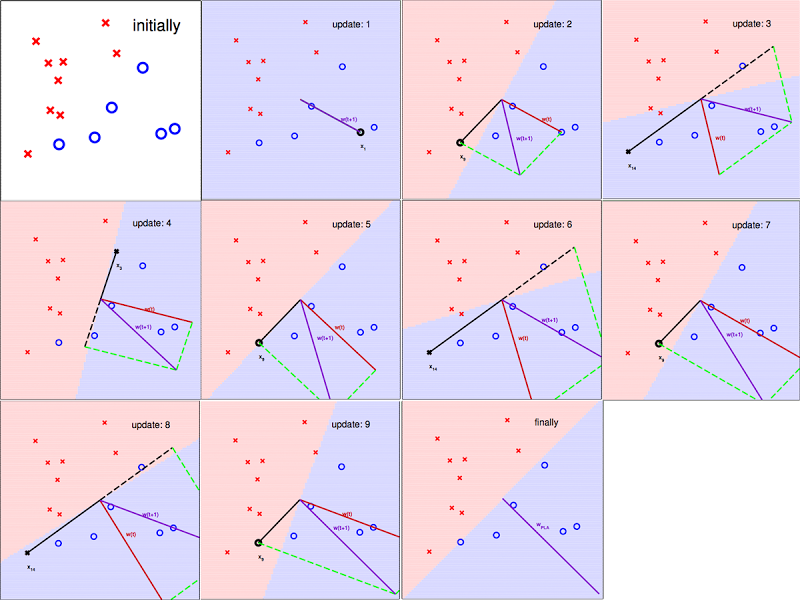
  图3 PLA 知“错”就“改”的过程

  从图中可以看出$w$确实在PLA的指导下，慢慢接近心目中的$w_f$。

  我们知道在数据线性可分的前提下，我们心目中有个完美的$w_f$，它能够完美的把圈圈和叉叉区分开来。那么如何证明PLA能够使$w$不断接近$w_f$呢？

  这里就要用到夹角余弦的公式，如果$w_t$更新之后的$w_{t+1}$与$w_f$之间的夹角余弦变大(夹角变小)了，则我们可以说PLA是有效的。首先我们先来看pla的几个性质:

---

1. 因为$w_f$是完美的，因此对于任意的$x_n$，$w_f$都能把它归入正确的类别:

   $y_{n(t)}w_f^Tx_{n(t)} \geq min\ {y_nw_f^Tx_n} \gt 0$
   
   

2. $w_f^Tw_t$在更新了任何一个错误点$(x_{n(t)},y_{n(t)})$后都会增大: $$\begin{equation} \begin{split} w_f^Tw_{t+1} &= w_f^T(w_t+y_{n(t)}x_{n(t)}) \\\ &\geq w_f^Tw_t + min\ {y_nw_f^Tx_n} \\\ &\gt w_f^Tw_t \end{split} \end{equation}$$

3. 看起来$w_{t+1}$是更接近$w_f$了，但他们内积的增大并不能表示他们夹角的变小，也有可能是因为$w_{t+1}$长度$||w_{t+1}||$增大了。但是$||w_{t+1}||$的增加是有限的:

   $$\begin{equation} \begin{split} ||w_{t+1}||^2 &= ||w_t + y_{n(t)}x_{n(t)}||^2 \\\ &= ||w_t||^2 + 2y_{n(t)}w_t^Tx_{n(t)} + ||y_{n(t)}x_{n(t)}||^2\\\ &\leq ||w_t||^2 + 0 + ||y_{n(t)}x_{n(t)}||^2 \\\ &\leq ||w_t||^2 + max\ {||x_n||^2} \end{split} \end{equation}$$

---

  根据上面的性质，我们可以来求夹角余弦。从$w_0=0$(初始的向量)开始，经过T次错误更正，变为$w_T$，那么就有:

$$\begin{equation} \begin{split} w_f^Tw_T &\geq w_f^Tw_{T-1} + min\ {y_nw_f^Tx_n} \\\ &\geq ... \\\ &\geq w_f^Tw_0 + T\cdot min\ {y_nw_f^Tx_n} = T\cdot min\ {y_nw_f^Tx_n} \end{split} \end{equation}$$ $$\begin{equation} \begin{split} ||w_T||^2 &\leq ||w_{T-1}||^2 + max\ {||x_n||^2} \\\ &\leq ... \\\ &\leq ||w_0||^2 + T\cdot max\ {||x_n||^2} = T\cdot max\ {||x_n||^2} \end{split} \end{equation}$$

  再来求$w_T$与$w_f$的夹角余弦:
$$
\begin{equation}
\begin{split}
\frac{w_f^Tw_T}{||w_f||||w_T||} &\geq \frac{T\cdot min\ y_nw_f^Tx_n}{||w_f||||w_T||} \
&\geq \frac{T\cdot min\ y_nw_f^Tx_n}{||w_f||\cdot \sqrt{T}\cdot max\ {||x_n||^2}}
= \frac {\sqrt{T}\rho}{R}
\end{split}
\end{equation}
$$

  其中$\rho = min\ y_n\frac {w_f^T}{||w_f||}x_n$与$R^2 = max\ {||x_n||^2}$都是大于0的常数。由于夹角余弦是小于等于1的，因此有:

$$1 \geq \frac{w_f^Tw_T}{||w_f||||w_T||} \geq \frac {\sqrt{T}\rho}{R}$$

  上面的不等式告诉我们两点:

1. PLA能够帮助$w_T$进步，因为$w_T$与$w_f$的夹角余弦随着更新错误点的次数T的增加而增加，$w_T$越来越接近$w_f$。

2. PLA会停止(halt)，因为$T \leq R^2/\rho ^2$，即当数据是线性可分时，经过有限次数的迭代，一定能找到一个能够把数据完美区分开的perceptron。

Pocket Step - 把最好的$w$放口袋

---

  有时我们拿到的数据数量庞大，或是不是线性可分的，这个时候用PLA将消耗大量的时间，或是根本无法停止，这个时候我们可以使用一种委曲求全的办法，在PLA中加入pocket step。这个pocket是做什么用的呢？这个pocket会使用PLA在每次迭代中产生的$w$，带进原始数据，去计算分类错误率，并记录最好的那个$w$，譬如我们设定让PLA迭代N次就停止，则pocket返回这N次迭代中出现的最好的$w$。当N足够大的时候，pocket总能返回还不错的结果。