机器学习笔记

笔记整理自台大林轩田老师的开放课程-机器学习基石，笔记中所有图片来自于课堂讲义。

  上一篇讲到了VC Dimension以及VC Bound。VC Bound所描述的是在给定数据量N以及给定的Hypothesis Set的条件下，遇到坏事情的概率的上界，即$E_{in}$与$E_{out}$差很远的概率，最多是多少。VC Bound用公式表示就是：

$$\begin{aligned} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \end{aligned}$$

  其中$m_{\mathcal{H}}(N)$为Hypothesis Set的成长函数，有：

$$\begin{aligned} \\m_{\mathcal{H}}(N)\leq \sum_{i=0}^{d_{vc}}\binom {N}{i}\leq N^{d_{vc}} \\\ \textit{( for }N\geq 2, d_{vc}\geq 2\textit{ )} \end{aligned}$$

  因为寻找所有Hypothesis Set的成长函数是困难的，因此我们再利用$N^{d_{vc}}$来bound住所有VC Dimension为$d_{vc}$的Hypothesis Set的成长函数。所以对于任意一个从$\mathcal{H}$中的$g$来说，有：

$$\begin{aligned} &\;\;\;\,\mathbb{P}[|E_{in}(g) - E_{out}(g)\gt \epsilon|] \\\ &\leq \mathbb{P}[BAD]\\\ &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \\\ &\leq 4(2N)^{d_{vc}}exp(-\frac{1}{8}\epsilon^2N) \\\ &\textit{( if }d_{vc}\textit{ is finite )} \end{aligned}$$

  因此说想让机器真正学到东西，并且学得好，有三个条件：

1. $\mathcal{H}$的$d_{vc}$是有限的，这样VC Bound才存在。(good $\mathcal{H}$)
2. $N$足够大(对于特定的$d_{vc}而言$)，这样才能保证上面不等式的bound不会太大。(good $\mathcal{D}$)
3. 算法$\mathcal{A}$有办法在$\mathcal{H}$中顺利地挑选一个使得$E_{in}$最小的方程$g$。(good $\mathcal{A}$)

  为什么要费那么大的力气来讲这个VC Bound和VC Dimension呢？因为对于初学者来说，最常犯的错误就是只考虑到了第3点，而忽略掉了前两点，往往能在training set上得到极好的表现，但是在test set中表现却很烂。关于算法$\mathcal{A}$的部分会在后续的笔记当中整理，目前我们只关心前面两点。

几种Hypothesis Set的VC Dimension

  对于以下几个$\mathcal{H}$，由于之前我们已经知道了他们的成长函数(见机器学习笔记-VC Dimension, Part I)，因此可以根据$m_{\mathcal{H}}(N)\leq N^{d_{vc}}$，直接得到他们的VC Dimension：

• positive rays: $m_{\mathcal{H}}(N)=N+1$，看N的最高次项的次数，知道$d_{vc}=1$
• positive intervals: $m_{\mathcal{H}}(N)=\frac{1}{2}N^2+\frac{1}{2}N+1$，$d_{vc}=2$
• convex sets: $m_{\mathcal{H}}(N)=2^N$，$d_{vc}=\infty$
• 2D Perceptrons: $m_{\mathcal{H}}(N)\leq N^3\;for\;N\geq 2$，所以$d_{vc}=3$

  由于convex sets的$d_{vc}=\infty$，不满足上面所说的第1个条件，因此不能用convex sets这个$\mathcal{H}$来学习。

  但这里要回归本意，通过成长函数来求得$d_{vc}$没有太大的意义，引入$d_{vc}$很大的一部分原因是，我们想要得到某个Hypothesis Set的成长函数是困难的，希望用$N^{d_{vc}}$来bound住对应的$m_{\mathcal{H}}(N)$。对于陌生的$\mathcal{H}$，如何求解它的$d_{vc}$呢？

某个$\mathcal{H}$的VC Dimension - 从"shatter"的角度

  Homework当中的某题，求解简化版决策树的VC Dimension：

Consider the simplified decision trees hypothesis set on $\mathbb{R}^d$, which is given by

$$\begin{aligned} \mathcal{H} = \{&h_{t,S}\; |\; h_{t,S} = 2[v \in S] - 1, \text{where } v_i=[x_i\gt t_i], \\\ &\textbf{S}\text{ is a collection of vectors in }\{0,1\}^d, \textbf{t}\in \mathbb{R}^d \} \end{aligned}$$

That is, each hypothesis makes a prediction by first using the $d$ thresholds $t_i$ to locate $x$ to be within one of the $2^d$ hyper-rectangular regions, and looking up $S$ to decide whether the region should be +1 or −1. What is the VC-dimension of the simplified decision trees hypothesis set?

  如何去理解题意呢？用一个2维的图来帮助理解：

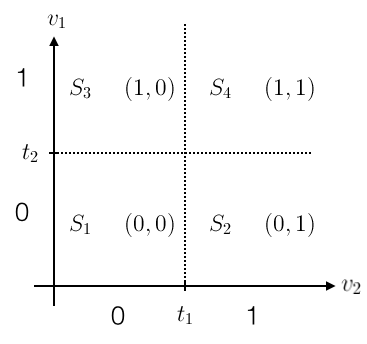
  首先把二维实数空间$\mathbb{R}^2$中的向量$x$，通过各个维度上的阈值$t_i$，转换到${\{0,1\}}^2$空间下的一个点$v$，规则为$v_i=[x_i\gt t_i]$。譬如对于$t=[5,10]$，$x=[6,8]$可以转换为新的空间下的$[1,0]$。这样一来，原来的$\mathbb{R}^2$空间就可以被划分为4个区块$S_1$~$S_4$（hyper-rectangular regions）。$\mathcal{H}$中每一个方程$h$代表着一种对这4块区域是”圈圈“还是”叉叉“的决策(decision)，并且这4块区域的决策是互相独立的，$S_1$的决策是”圈圈“还是”叉叉“和$S_2,S_3,S_4$都没有关系。

  由于这4块区域的决策是互相独立的，那么它最多最多能shatter掉多少个点呢？4个，(当这4个点分别属于这4块区域的时候)，即这4块hyper-rectangular regions所代表的类别可以是(o,o,o,o)、(o,o,o,x)、(o,o,x,o)、...、(x,x,x,x),共16种可能，因此它能够shatter掉4个点。

  由上面2维的例子我们可以看出，simplified decision trees的VC Dimension，等于hyper-rectangular regions的个数。$d$维空间$\mathbb{R}^d$可以用$d$条直线切分出$2^d$个互相独立的hyper-rectangular regions，即最多最多可以shatter掉$2^d$个点，因此simplified decision trees的$d_{vc}=2^d$。

  我们再来回顾一下Positive Intervals：

  也可以按照上面的方法去理解，Positive Intervals有两个thresholds，把直线切分为3块空间。但这3块空间并不是相互独立，中间的部分永远是+1，左右两边永远是-1，所以还要具体看它能够shatter掉多少个点，这里最多最多只能shatter掉2个点，它的$d_{vc}=2$。

某个$\mathcal{H}$的VC Dimension - 从"自由度"的角度

  对于$d_{vc}$较小的$\mathcal{H}$，可以从它最多能够shatter的点的数量，得到$d_{vc}$，但对于一些较为复杂的模型，寻找能够shatter掉的点的数量，就不太容易了。此时我们可以通过模型的自由度，来近似的得到模型的$d_{vc}$。

  维基百科上有不止一个关于自由度的定义，每种定义站在的角度不同。在这里，我们定义自由度是，模型当中可以自由变动的参数的个数，即我们的机器需要通过学习来决定模型参数的个数。

  譬如：

• Positive Rays，需要确定1个threshold，这个threshold就是机器需要根据$\mathcal{D}$来确定的一个参数，则Positive Rays中自由的参数个数为1，
• Positive Intervals，需要确定左右2个thresholds，则可以由机器自由决定的参数的个数为2，$d_{vc}=2$
• d-D Perceptrons，$d$维的感知机，可以由机器通过学习自由决定的参数的个数为$d+1$（别忘了还有个$w_0$），$d_{vc}=d+1$

多个$\mathcal{H}$的并集的VC Dimension

  Homework当中某题，求$K$个Hypothesis Set的并集$d_{vc}(\cup_{k=1}^{K}\mathcal{H}_k)$的VC Dimension的上下界。下界比较好判断，是$max\\{d_{vc}(\mathcal{H}_k)\\}_{k=1}^K$，即所有的$\mathcal{H}$都包含于$d_{vc}$最大的那个$\mathcal{H}$当中的时候。上界则出现在各个$\mathcal{H}$互相都没有交集的时候，我们不妨先来看看$K=2$的情况：

  求$d_{vc}(\mathcal{H}_1\cup \mathcal{H}_2)$的上界，已知$d_{vc}(\mathcal{H}_1)=d_1$，$d_{vc}(\mathcal{H}_2)=d_2$。

  从成长函数上看，有 $m_{\mathcal{H}_1\cup \mathcal{H}_2}(N) \leq m_{\mathcal{H}_1}(N) + m_ {\mathcal{H}_2}(N)$，把成长函数展开，有

$$m _ {\mathcal{H}_1\cup \mathcal{H}_2}(N) \leq \sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=0} ^ {d_2} \binom{N}{i}$$

  用$\binom{N}{i}=\binom{N}{N-i}$替换RHS，有

$$m _ {\mathcal{H}_1\cup \mathcal{H}_2}(N) \leq \sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=0} ^ {d_2} \binom{N}{N-i} \leq \sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=N-d_2} ^ {N} \binom{N}{i}$$

  我们可以尝试寻找下上面这个成长函数有可能的最大的break point，让$N$不断增大，直到出现$m_{\mathcal{H}_1\cup \mathcal{H}_2}(N)\lt 2^N$的时候，这个$N$就是break point。那么$N$要多大才够呢？

  $N=d_1$够大吗？不够，因为：

$$\sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=N-d_2} ^ {N} \binom{N}{i} = 2^N + \sum _ {i=N-d_2} ^ {N} \binom{N}{i} \gt 2^N$$

  $N=d_1+d_2+1$够大吗？还是不够，因为：

$$\sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=N-d_2} ^ {N} \binom{N}{i} = \sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=d_1+1} ^ {N} \binom{N}{i} = 2^N$$

  $N=d_1+d_2+2$够大吗？够大了，因为：

$$\sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=N-d_2} ^ {N} \binom{N}{i} = \sum _ {i=0} ^ {d_1} \binom{N}{i} + \sum _ {i=d_1+2} ^ {N} \binom{N}{i} = 2^N - \binom{N}{d_1+1} \lt 2^N$$

  所以$m_{\mathcal{H}_1\cup \mathcal{H}_2}(N)$的break point最大可以是$d_1+d_2+2$，此时$d_{vc}(\mathcal{H}_1\cup \mathcal{H}_2)=d_1+d_2+1$。

  因此两个$\mathcal{H}$的并集的VC Dimension的上界为$d_{vc}(\mathcal{H}_1)+d_{vc}(\mathcal{H}_2)+1$。利用此方法，就很容易可以推出$K$个$\mathcal{H}$的并集的情况。

简单 v.s 复杂

  机器学习笔记-VC Dimension, Part I一开始就提到，learning的问题应该关注的两个最重要的问题是：1.能不能使$E_{in}$与$E_{out}$很接近，2.能不能使$E_{in}$足够小。

• 对于相同的$\mathcal{D}$而言，$d_{vc}$小的模型，其VC Bound比较小，比较容易保证$E_{in}$与$E_{out}$很接近，但较难做到小的$E_{in}$，试想，对于2D Perceptron，如果规定它一定要过原点($d_{vc}=2$)，则它就比没有规定要过原点($d_{vc}=3$)的直线更难实现小的$E_{in}$，因为可选的方程更少。2维平面的直线，就比双曲线($d_{vc}=6$)，更难实现小的$E_{in}$。
• 对于相同的$\mathcal{D}$而言，$d_{vc}$大的模型，比较容易实现小的$E_{in}$，但是其VC Bound就会很大，很难保证模型对$\mathcal{D}$之外的世界也能有同样强的预测能力。

  令之前得到的VC Bound为$\delta$，坏事情$[|E_{in}(g)-E_{out}(g)|\gt \epsilon]$发生的概率小于$\delta$，则好事情$[|E_{in}(g)-E_{out}(g)|\leq \epsilon]$发生的概率就大于$1-\delta$，这个$1-\delta$在统计学中又被称为置信度，或信心水准。

$$\begin{aligned} \text{set}\;\;\;\;\delta &= 4(2N)^{d_{vc}}exp(-\frac{1}{8}\epsilon^2N)\\\ \sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} &= \epsilon \end{aligned}$$

  因此$E_{in}$、$E_{out}$又有下面的关系：

$$E_{in}(g)-\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \leq E_{out}(g) \leq E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})}$$

  令$\Omega (N,\mathcal{H},\delta)=\sqrt{...}$，即上式的根号项为来自模型复杂度的，模型越复杂，$E_{in}$与$E_{out}$离得越远。

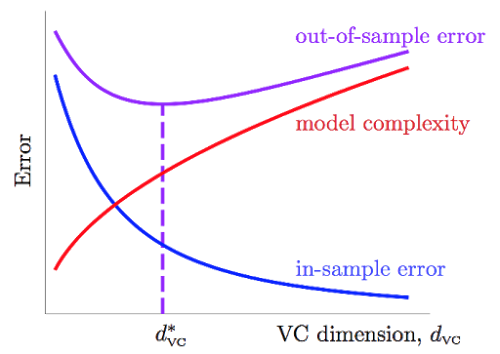
  随着$d_{vc}$的上升，$E_{in}$不断降低，而$\Omega$项不断上升，他们的上升与下降的速度在每个阶段都是不同的，因此我们能够寻找一个二者兼顾的，比较合适的$d_{vc}^{*}$，用来决定应该使用多复杂的模型。

  反过来，如果我们需要使用$d_{vc}=3$这种复杂程度的模型，并且想保证$\epsilon = 0.1$，置信度$1-\delta =90\%$，我们也可以通过VC Bound来求得大致需要的数据量$N$。通过简单的计算可以得到理论上，我们需要$N\approx 10,000d_{vc}$笔数据，但VC Bound事实上是一个极为宽松的bound，因为它对于任何演算法$\mathcal{A}$，任何分布的数据，任何目标函数$f$都成立，所以经验上，常常认为$N\approx 10d_{vc}$就可以有不错的结果。