前面花了很大篇幅在说机器为何能学习，接下来要说的是机器是怎么学习的，进入算法$\mathcal{A}$的部分。上一篇稍微提到了几个error的衡量方式，接下来的几篇笔记要讲的就是各种error measurement的区别以及针对它们如何设计最优化的算法。通过设计出来的算法，使得机器能够从$\mathcal{H}$(Hypothesis Set)当中挑选可以使得cost function最小的$h$作为$g$输出。

  本篇以众所周知的线性回归为例，从方程的形式、误差的衡量方式、如何最小化$E_{in}$的角度出发，并简单分析了Hat Matrix的性质与几何意义，希望对线性回归这一简单的模型有个更加深刻的理解。

方程的形式：

$$h(x)=\sum_{i=\color{red}{0}}^d w_ix_i= w^Tx \\\ $$

  长得很像perceptron(都是直线嘛)，perceptron是$h(x)=sign(w^Tx)$。

误差的衡量 — 平方误差(squared error)：

$$\begin{matrix} err(\hat{y}_n,y_n) = (\hat{y}_n-y_n)^2\\\ (\hat{y}_n\text{为预测值，}y_n\text{为真实值}) \end{matrix}$$

Cost function：

$$E_{in}(w)=\frac{1}{N}\sum_{n=1}^N(\hat{y}_n - y_n)=\frac{1}{N}\sum_{n=1}^N(w^Tx_n-y_n)^2$$

  $h(x)$是一个以$x$为变量的方程，而$E_{in}(w)$变成了一个以$w$为变量的方程。这样一来，我们就把“在$\mathcal{H}$中寻找能使平均误差最小的方程”这个问题，转换为“求解一个函数的最小值”的问题。使得$E_{in}(w)$最小的$w$，就是我们要寻找的那个最优方程的参数。

如何最小化$E_{in}(w)$：

  用矩阵形式表示：

$$\begin{aligned} E_{in}(\color{blue}{w}) &= \frac{1}{N}\sum_{n=1}^{N}(\color{blue}{w^T}\color{red}{x_n}-\color{purple}{y_n})^2=\frac{1}{N}\sum_{n=1}^{N}(\color{red}{x_n^T}\color{blue}{w}-\color{purple}{y_n})^2 \\\ &=\frac{1}{N}\begin{Vmatrix} \color{red}{x_1^T}\color{blue}{w}-\color{purple}{y_1}\\\ \color{red}{x_2^T}\color{blue}{w}-\color{purple}{y_2}\\\ ...\\\ \color{red}{x_N^T}\color{blue}{w}-\color{purple}{y_N} \end{Vmatrix}^2 \\\ &=\frac{1}{N}\begin{Vmatrix} \color{red}{\begin{bmatrix} --x_1^T--\\\ --x_2^T--\\\ ...\\\ --x_N^T-- \end{bmatrix}} \color{blue}{w} - \color{purple}{\begin{bmatrix} y_1\\\ y_2\\\ ...\\\ y_3 \end{bmatrix}} \end{Vmatrix}^2 \\\ &=\frac{1}{N}|| \underbrace{\color{red}{X}}_{N\times d+1}\;\;\; \underbrace{\color{blue}{w}}_{d+1\times 1} \; - \; \underbrace{\color{purple}{y}}_{N\times 1} ||^2 \end{aligned}$$

  $\color{red}{X}$与$\color{purple}{y}$来源于$\mathcal{D}$，是固定不变的，因此它是一个以$\color{blue}{w}$为变量的函数。我们需要解使得$E_{in}$最小的$\color{blue}{w}$，即$\underset{\color{blue}{w}}{min}\,E_{in}(\color{blue}{w})=\frac{1}{N}\begin{Vmatrix}\color{red}{X}\color{blue}{w}-\color{purple}{y}\end{Vmatrix}^2$。这个$E_{in}(\color{blue}{w})$是一个连续(continuous)、处处可微(differentiable)的凸函数(convex)：

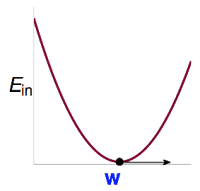
  对于这一类函数，只需要解其一阶导数为0时的解即可。

$$E_{in}(\color{blue}{w}) \equiv \begin{bmatrix} \frac{\partial E_{in}}{\partial \color{blue}{w}_0}(\color{blue}{w})\\\ \frac{\partial E_{in}}{\partial \color{blue}{w}_1}(\color{blue}{w})\\\ ...\\\ \frac{\partial E_{in}}{\partial \color{blue}{w}_d}(\color{blue}{w}) \end{bmatrix}=\begin{bmatrix} \color{orange}{0}\\\ \color{orange}{0}\\\ ...\\\ \color{orange}{0} \end{bmatrix}$$

  关于多元函数的求导，就是线性代数的范畴了：

$$\boxed { \begin{matrix} \text{一元的情况}\\\ \\\ E_{in}(\color{blue}{w})=\frac{1}{N}(\color{red}{a}\color{blue}{w^2}-2\color{brown}{b}\color{blue}{w}+\color{purple}{c})\\\ \nabla E_{in}(\color{blue}{w})=\frac{1}{N}(2\color{red}{a}\color{blue}{w}-2\color{brown}{b}) \end{matrix} } \xrightarrow{\text{推广至}} \boxed{ \begin{matrix} \text{多元的情况}\\\ \\\ E_{in}(\color{blue}{w})=\frac{1}{N}(\color{blue}{w^T}\color{red}{A}\color{blue}{w}-2\color{blue}{w^T}\color{brown}{b}+\color{purple}{c})\\\ \nabla E_{in}(\color{blue}{w})=\frac{1}{N}(2\color{red}{A}\color{blue}{w}-2\color{brown}{b}) \end{matrix} }$$

  所以有：

$$\begin{aligned} \nabla E_{in}(\color{blue}{w}) &=\nabla \frac{1}{N}(\color{blue}{w^T}\color{red}{X^TX}\color{blue}{w}-2\color{blue}{w^T}\color{brown}{X^Ty}+\color{purple}{y^Ty}) \\\ &=\frac{2}{N}(\color{red}{X^TX}\color{blue}{w}-\color{brown}{X^Ty}) \end{aligned}$$

  令$\nabla E_{in}(\color{blue}{w})=0$，可得最佳解：

$$\color{blue}{w_{LIN}}=\underbrace{(\color{red}{X^TX})^{-1}\color{red}{X^T}}_{pseudo-inverse\;\color{red}{X^{\dagger}}}\;\;\;\color{purple}{y} = \color{red}{X^{\dagger}} \color{purple}{y}$$

  当$\color{red}{X^TX}$可逆的时候用它作为pseudo-inverse矩阵$\color{red}{X^{\dagger}}$，当$\color{red}{X^TX}$不可逆的时候，再用其他方式定义$\color{red}{X^{\dagger}}$，这里就不详述了。

  用以$\color{blue}{w_{LIN}}$为参数的线性方程对原始数据做预测，可以得到拟合值$\hat{y}=\color{red}{X}\color{blue}{w_{LIN}}=\color{red}{XX^{\dagger}}\color{purple}{y}$。这里又称$\color{orange}{H}=\color{red}{XX^{\dagger}}$为Hat Matrix，帽子矩阵，$\color{orange}{H}$为$\color{purple}{y}$带上了帽子，成为$\hat{y}$，很形象吧。

Hat Matrix 的几何意义

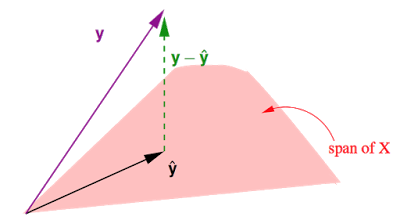
  这张图展示的是在N维实数空间$\mathbb{R}^N$中，注意这里是N=数据笔数，$\color{purple}{y}$中包含所有真实值，$\hat{y}$中包含所有预测值，与之前讲的输入空间是d+1维是不一样的噢。$\color{red}{X}$中包含d+1个column：

• $\hat{y}=\color{red}{X}\color{blue}{w_{LIN}}$是$\color{red}{X}$的一个线性组合，$\color{red}{X}$中每个column对应$\mathbb{R}^N$下的一个向量，共有d+1个这样的向量，因此$\hat{y}$在这d+1个向量所构成的$\color{red}{span}$(平面)上。
• 事实上我们要做的就是在这个平面上找到一个向量$\hat{y}$使得他与真实值之间的距离$|\color{green}{y-\hat{y}}|$最短。不难发现当$\hat{y}$是$\color{purple}{y}$在这个平面上的投影时，即$\color{green}{y-\hat{y}}\perp \color{red}{span}$时，$|\color{green}{y-\hat{y}}|$最短。
• 所以之前说过的Hat Matrix $\color{orange}{H}$，为$\color{purple}{y}$戴上帽子，所做的就是投影这个动作，寻找$\color{red}{span}$上$\color{purple}{y}$的投影。
• $\color{orange}{H}\color{purple}{y}=\hat{y}$，$(I-\color{orange}{H})\color{purple}{y}=\color{green}{y-\hat{y}}$。($I$为单位矩阵)

  下面来探究一下$\color{orange}{H}$的性质，这个很重要噢。

$$\text{Hat Matrix }\color{orange}{H} = \color{red}{X(X^TX)}^{-1}\color{red}{X^T}$$

• 对称性(symetric)，即$\color{orange}{H}=\color{orange}{H^T}$：

$$\begin{aligned} \color{orange}{H^T} &= (\color{red}{X(X^TX)}^{-1}\color{red}{X^T})^T \\\ &=\color{red}{X({(X^TX)}^{-1})^TX^T} \\\ &=\color{red}{\color{red}{X(X^TX)}^{-1}\color{red}{X^T}}\\\ &=\color{orange}{H} \end{aligned}$$

• 幂等性(idempotent)，即$\color{orange}{H^2}=\color{orange}{H}$：

$$\begin{aligned} \color{orange}{H^2} &= (\color{red}{X(X^TX)}^{-1}\color{red}{X^T})(\color{red}{X(X^TX)}^{-1}\color{red}{X^T})\\\ &=\color{red}{X\;}\underbrace{\color{red}{(X^TX)}^{-1}\color{red}{(X^TX)}}_{I}\;\color{red}{(X^TX)}^{-1}\color{red}{X^T} \\\ &=\color{red}{X}\color{red}{(X^TX)}^{-1}\color{red}{X^T}\\\ &=\color{orange}{H} \end{aligned}$$

• 半正定(positive semi-definite)，即所有特征值为非负数：
  (以下$\lambda$为特征值，$b$为对应的特征向量)

$$\begin{aligned} \color{orange}{H}b&=\lambda b\\\ \color{orange}{H^2}b&=\lambda \color{orange}{H}b \\\ &=\lambda (\lambda b)\\\ \text{(因为}\color{orange}{H^2}&=\color{orange}{H}\text{)}\\\ \color{orange}{H^2}b&=\color{orange}{H}b=\lambda b\\\ \text{所以}&:\\\ \lambda ^2b&=\lambda b \\\ \text{即}&:\\\ \lambda (\lambda -1)b&=0 \\\ \lambda = 0 &\text{ or } \lambda=1 \end{aligned}$$

  林老师在课堂上讲到：

$$trace(I-\color{orange}{H}) = N-(d+1)$$

  $trace$为矩阵的迹。这条性质很重要，但是为什么呢？证明过程有点多，以后有机会再补充，心急的同学可以看这里[General formulas for bias and variance in OLS][4]。一个矩阵的$trace$等于该矩阵的所有特征值(Eigenvalues)之和。

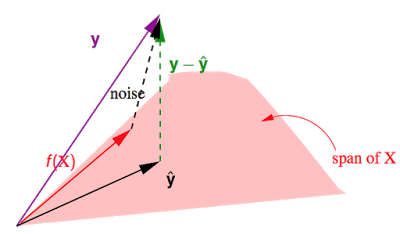
  假设$\color{purple}{y}$由$\color{red}{f(X)\in span}+noise$构成的。有$\color{purple}{y}=\color{red}{f(X)}+noise$。之前讲到$\color{orange}{H}$作用于某个向量，会得到该向量在$\color{red}{span}$上的投影，而$I-\color{orange}{H}$作用于某个向量，会得到那条与$\color{red}{span}$垂直的向量，在这里就是图中的$\color{green}{y-\hat{y}}$，即$(I-\color{orange}{H})noise=\color{green}{y-\hat{y}}$。

  这个$\color{green}{y-\hat{y}}$是真实值与预测值的差，其长度就是就是所有点的平方误差之和。于是就有：

$$\begin{aligned} E_{in}(\color{blue}{w_{LIN}})&=\frac{1}{N}||\color{green}{y-\hat{y}}||^2\\\ &=\frac{1}{N}||(I-\color{orange}{H})noise||^2 \\\ &=\frac{1}{N}trace(I-\color{orange}{H})||noise||^2 \\\ &=\frac{1}{N}(N-(d+1))||noise||^2 \end{aligned}$$

  上面的证明不太好整理进来，依然可以参考General formulas for bias and variance in OLS。

  因此，就平均而言，有：

$$\begin{aligned} \color{red}{\overline{E_{in}}}&=\text{noise level}\cdot(1-\frac{d+1}{N})\\\ \color{blue}{\overline{E_{out}}}&=\text{noise level}\cdot(1+\frac{d+1}{N}) \;\;\;(后面这个不懂证了。) \end{aligned}$$

  花这么大力气是为了什么，又回到之前learning可行性的话题了。

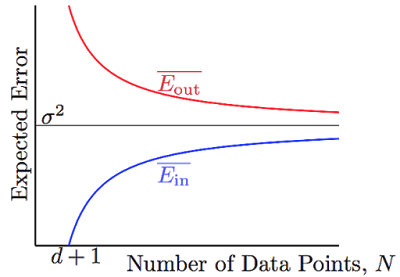
  $\color{red}{\overline{E_{in}}}$和$\color{blue}{\overline{E_{out}}}$都向$\sigma ^2$(noise level)收敛，并且他们之间的差异被$\frac{2(d+1)}{N}$给bound住了。有那么点像VC bound，不过要比VC bound来的更严格一些。