笔记整理自台大林轩田老师的开放课程-机器学习基石，笔记中所有图片来自于课堂讲义。

  前面的笔记所谈到的分类模型，都是基于线性的，即我们假设数据是线性可分，或者至少看起来用一条线来做分类是不错的。但现实中我们的数据往往不那么容易得能用一条线区分开来。

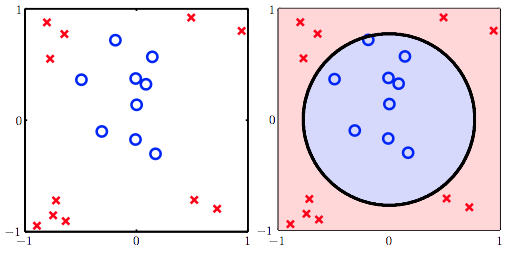
  可以发现$\mathcal{D}$并不是一个线性可分的数据，但使用一个圆圈，却可以很好得把圈圈和叉叉区分开来。这个”圆圈分类器”可以是下面这种形式:

$$h_{SEP}(x)=sign(-x_1^2-x_2^2+0.6)$$

  看样子我们需要重新设计分类模型与算法，做一个圆圈版本的PLA，圆圈版本的Regression。所以接下来几篇笔记应该是$\color{orange}{\text{Circular}}-\text{PLA}$、$\color{orange}{\text{Circular}}-\text{Regression}$。事实上是不需要这么麻烦的，下面我们来分析下那个圈圈分类器的方程：

$$\begin{aligned} \color{orange}{h}(x) &= (\; \underbrace{\color{orange}{0.6}}_{\color{orange}{\tilde{w}_0}}\cdot\underbrace{\color{purple}{1}}_{\color{purple}{z_0}} + \underbrace{(\color{orange}{-1})}_{\color{orange}{\tilde{w}_1}}\cdot\underbrace{\color{purple}{x_1^2}}_{\color{purple}{z_1}}+ \underbrace{(\color{orange}{-1})}_{\color{orange}{\tilde{w}_2}}\cdot\underbrace{\color{purple}{x_2^2}}_{\color{purple}{z_2}} \;) \\\ &= sign(\color{orange}{\tilde{w_0}}+\color{orange}{\tilde{w_1}}\color{purple}{z_1}+\color{orange}{\tilde{w_2}}\color{purple}{z_2}) \\\ &=sign(\color{orange}{\tilde{w}^T}\color{purple}{z}) \end{aligned}$$

非线性变换

  如果我们只看包含$\color{purple}{z}$的部分，它事实上依然是一个线性方程。即，$\mathcal{X}$空间下的一个圆圈，对应到$\mathcal{Z}$空间下的一条直线。

  这个转换的过程成为nonlinear feature transform，用符号$\phi$表示，$\phi$把两个互相独立的空间给联系了起来:

$$(1,x_1^2,x_2^2)=\color{purple}{\phi}(x)=\color{purple}{(z_0,z_1,z_2)}=\color{purple}{z}$$

  $\mathcal{X}$空间下的每个点，都对应$\mathcal{Z}$空间下的某个点，同样的，$\mathcal{X}$空间下的二次曲线方程，都对应$\mathcal{Z}$空间下的某个一次直线方程。

$$h(x)=sign(\color{orange}{\tilde{w}_0}+\color{orange}{\tilde{w}_1}\color{purple}{x_1^2}+\color{orange}{\tilde{w}_2}\color{purple}{x_2^2})=sign(\color{orange}{\tilde{w}^T}\color{purple}{\phi}(x))=\color{orange}{\tilde{h}(\color{purple}{z})}$$

  这样以来，两个空间，在“冥冥之中”，产生了关联，前面说的$\phi$就是这两个空间的纽带，在这个纽带下，$\mathcal{Z}$空间下的不同直线也就对应$\mathcal{X}$下的不同形态的分类器。

$\tilde{w}$	X空间下的曲线形态
(0.6,−1,−1)	circle(圈圈在内部，叉叉在外部)
(−0.6,+1,+1)	circle(圈圈在外部，叉叉在内部)
(0.6,−1,−2)	ellipse
(0.6,−1,+2)	hyperbola
(0.6,+1,+2)	所有点都判断为圈圈

  更加一般化，我们把一次空间$\mathcal{X}$映射到二次空间$\mathcal{Z}$的时候，还会保留其一次项，即下面这个样子的映射才是完整的二次映射:

$$\color{purple}{\phi}(x)=(\color{purple}{1,x_1,x_2,x_1^2,x_1x_2,x_2^2})$$

  这样一来，这个完整版的$\mathcal{Z}$空间的直线，就可以代表$\mathcal{X}$空间下的所有二次曲线了。

  说了这么多，我们回想一下，我们为何要做这个非线性变换？逻辑是这样的：

• 在$\mathcal{X}$空间中，我们使用一条直线，很难把圈圈和叉叉分开
• 但是如果我们使用一条曲线，可以很容易做到
• 可我们只学过找最优“直线”的算法，没有学过找最佳“曲线”的算法
• 我们有一个纽带$\phi$，它能够把$\mathcal{X}$空间中的所有曲线，对应到$\mathcal{Z}$空间中的曲线，反过来也可以根据$\mathcal{Z}$空间的一条直线，找到$\mathcal{X}$空间中对应的曲线
• 所以我们可以把$\mathcal{X}$空间下的原始数据$\mathcal{D}$映射到$\mathcal{Z}$空间下
• 然后在$\mathcal{Z}$空间下寻找最佳的“直线”，找直线这件事我们已经学过该怎么做了
• 找到这条最佳的“直线”后，把它对应回$\mathcal{X}$空间，就是我们刚开始说的需要找的那条最佳的“曲线”了。

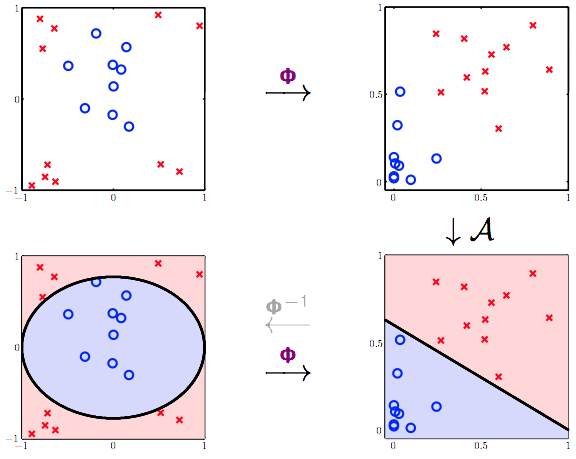
  实际操作上，分以下三步：

1. 变换原始数据 ${(x_n,y_n)}\Rightarrow {(\color{purple}{z_n}=\color{purple}{\phi}(x_n),y_n)}$
2. 利用之前学过的算法，使用${(\color{purple}{z_n},y_n)}$训练线性模型，得到$\color{orange}{\tilde{w}}$
3. 得到分类器方程$g(x)=sign(\color{orange}{\tilde{w}^T}\color{purple}{\phi_2}(x))$

非线性变换的代价

Q-th Order Polynomial Transform

  d维向量$x$经过Q次多项式变换:

$$\begin{matrix} \color{purple}{\phi}(x)=(&1, \\\ &\color{blue}{x_1,x_2,...,x_d,}\\\ &\color{blue}{x_1^2,x_1x_2,...,x_d^2},\\\ &...,\\\ &\color{blue}{x_1^Q,x_1^{Q-1}x_2,...,x_d^Q}\;) \end{matrix}$$

  (以上是Q次完整变换，当然我们不一定会需要完整项，譬如之前那个圆圈，就舍弃了$x_1x_2$项)
  若考虑完整变化，原来的$1+d$维向量经过变换，就成了$1+\tilde{d}=1+\binom{Q+d}{Q}$维向量，复杂度由$O(d)$变为$O(Q^d)$。

1. 计算变复杂，需要的存储空间增大

  这点很容易理解，如之前的例子，原始数据$(1,x_1,x_2)$经过变换之后变成$(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)$，需要多一倍的空间来存转换后的数据，同时参数的增加，也增大了计算量。

2. 模型复杂度增大

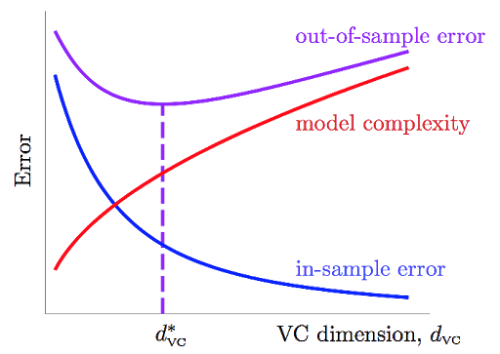
  之前的笔记VC Dimension, Part III，有讲到自由度与VC Dimension的关系，线性模型的$d_{vc}\approx 自由度 \approx \tilde{d}+1$。如果Q非常大的话，则模型的$d_{vc}$也会非常大，我们知道$d_{vc}$越大，越容易实现小的$E_{in}$，同时，也会造成$|E_{out}-E_{in}|$的加大，即模型的泛化能力(generalization)变差。

模型的泛化问题(Generalization Issue)

  上图是分别使用原始数据进行训练以及进行4次非线性变换后的数据进行训练的结果对比。从视觉上看，虽然右图(经过4次非线性变换的模型)能够把圈圈叉叉完全分开，但显然这种模型过于复杂了。
  很多时候我们会面临模型泛化能力和分类能力的权衡取舍，即：

$\tilde{d}(Q)$	$E_{out}(g)$能否与$E_{in}(g)$很接近?	$E_{in}(g)$是否足够小?
higher	:-(	:-D
lower	:-D	:-(

(表中符号若不理解，请把屏幕右转90度。XD)

  那么如何选择合适的复杂度呢？像上面一样用眼睛看？暂且不讨论10维的数据有没有办法用眼睛看，就拿前面2维的例子来说，用眼睛看来选择模型是件很危险的事情。

  在你没看数据之前，你决定要进行完整的2次非线性变换，即:

$$\phi_2(x)=(1,x_1,x_2,x_1^2,x_1x_2,x_2^2),d_{vc}=6$$

  不过你没有忍住，偷偷先看了下数据:

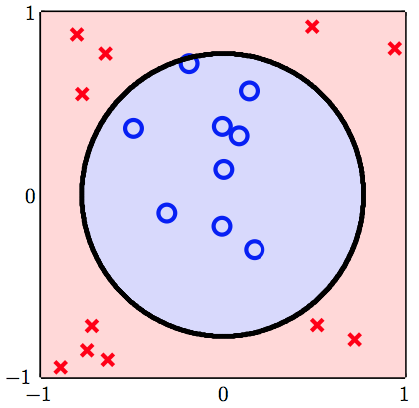
  发现，用一个圆圈，就可以达到理想的效果，于是你决定放弃$\phi_2$变换中的一些维度，即使用:

$$z=(1,x_1^2,x_2^2)\;,d_{vc}=3$$

  或者干脆了，你觉得一个正圆就够了，使用:

$$z=(1,x_1^2+x_2^2)\;,d_{vc}=2$$

  最终你采用了$d_{vc}$最小的那个方案，因为根据前面说的，用这个正圆，可以完全分开，而且$d_{vc}=2$，并没有增大，真实两全其美。不过，这个时候，$d_{vc}$真的还是2吗？其实这个时候$d_{vc}$是比较难判断的，因为你是在“看过”数据之后，由你大脑选择的一个模型，这里要考虑到你大脑“选择模型”产生的一个复杂度，因为如果重新选取一部分数据，你有可能就不再挑选正圆模型了，事实上你的大脑不知不觉地参与到了模型参数估计上，偷偷地把2次变换中产生的其他项前面的系数，估计为0了。因此要切记，在$\phi$的选择之前，不可以偷偷去看数据。 倘若你在没看数据之前，就决定使用正圆，则此时，该模型的$d_{vc}=2$。

Structured Hypothesis Sets

  通常我们说的非线性变换，指的是多项式变换(Polynomial Transform)。用符号$\phi_Q$来表示$Q$次多项式变换:

$$\begin{align*} \color{purple}{\phi_0}(x)=(1), \color{purple}{\phi_1}(x) &= (\phi_0(x),\color{blue}{x_1,x_2,...,x_d}) \\\ \color{purple}{\phi_2}(x) &= (\phi_1(x),\color{blue}{x_1^2,x_1x_2,...,x_d^2})\\\ \color{purple}{\phi_3}(x) &= (\phi_2(x),\color{blue}{x_1^3,x_1^2x_2,...,x_d^3})\\\ .&.....\\\ \color{purple}{\phi_Q}(x) &= (\phi_{Q-1}(x),\color{blue}{x_1^Q,x_1^{Q-1}x_2,...,x_d^Q}) \end{align*}$$

  可以发现$\phi_{i}(x)$中包含了$\phi_{i-1}(x)$，因此他们对应的Hypothesis Set也有如下关系:

$$\mathcal{H}_{\phi_0}\subset \mathcal{H}_{\phi_1} \subset \mathcal{H}_{\phi_2} \subset \mathcal{H}_{\phi_3} \subset \;...\; \subset \mathcal{H}_{\phi_Q}$$

  假如我们分别对原始数据进行$i$次非线性多项式变换并训练模型，$g_i$表示使用$i$次非线性多项式变换后的数据所训练出的最优模型，$\color{blue}{g_i=argmin_{h\in \mathcal{H}_i}E_{in}(h)}$则有:

$$\begin{matrix} \mathcal{H}_{\phi_0} &\subset &\mathcal{H}_{\phi_1} &\subset &\mathcal{H}_{\phi_2} &\subset &\mathcal{H}_{\phi_3} &\subset & ... \\\ \color{red}{d_{vc}(\mathcal{H}_0)}&\color{red}{\leq} &\color{red}{d_{vc}(\mathcal{H}_1}) &\color{red}{\leq} &\color{red}{d_{vc}(\mathcal{H}_2)} &\color{red}{\leq} &\color{red}{d_{vc}(\mathcal{H}_3)} &\color{red}{\leq} &\color{red}{...} \\\ \color{blue}{E_{in}(g_0)}&\color{blue}{\ge} & \color{blue}{E_{in}(g_1)}&\color{blue}{\ge} & \color{blue}{E_{in}(g_2)}&\color{blue}{\ge} & \color{blue}{E_{in}(g_3)}&\color{blue}{\ge} & \color{blue}{...} \end{matrix}$$

  通常在进行高次非线性变换的时候，应该特别小心，因为$d_{vc}$上升很快，极容易造成overfitting。比较安全的做法是，先尝试不做非线性变换，即使用$\mathcal{H}_{\phi_1}$，如果效果足够好了，就不需要进行非线性变换，如果效果不够好，再慢慢尝试使用复杂更高的模型。