本次实验是coursera上的一门课Data Analysis的一次小作业。将使用智能手机加速度传感器与三轴陀螺仪采集到的数据,来预测用户当前的活动(walking, walking_upstairs, walking_downstairs, sitting, standing, laying)。所用的数据可以从课程提供的链接下载,https://spark-public.s3.amazonaws.com/dataanalysis/samsungData.rda 。.rda为R专用的数据文件,在R中直接使用load()即可将其载入,比较方便。除此之外,也可到UCI Machine Learning Repository下载原始文件,当中包含dataset的中各个变量以及衍生变量的简介,数据格式为纯文本。
数据整理
先确定一下当前的工作路径。
1
| ## [1] "~/Dropbox/Homeworks/Data Analysis/DataAnalysisProject2/code"
|
我把samsungData.rda放在~/Dropbox/Homeworks/Data Analysis/DataAnalysisProject2/data中,.rda文件的好处就是直接load一遍就可以把当时储存在内存中的object全部载入,而不需要再从txt或者csv文件中读取数据了。
1
| load("../data/samsungData.rda")
|
一共有7352条记录,563个变量。
1 2
| length(unique(samsungData$subject))
|
这里subject代表志愿者编号,这里共有21个志愿者参与。
把所有变量的名称读出来,随便挑几个看看。
1 2 3
| cnames = names(samsungData) sample(cnames, 10)
|
1 2 3 4 5
| ## [1] "tBodyGyroJerk-arCoeff()-Z,4" "fBodyAccJerk-meanFreq()-X" ## [3] "fBodyAccJerk-skewness()-Y" "tBodyGyroJerk-arCoeff()-Y,3" ## [5] "fBodyGyro-bandsEnergy()-1,24" "tBodyAcc-std()-Z" ## [7] "tBodyGyroJerkMag-min()" "fBodyAccJerk-energy()-Y" ## [9] "tBodyAccMag-mad()" "fBodyAcc-kurtosis()-Z"
|
变量名称中有-,(),可能会使之后的分析工作出现异常,之后要把变量名处理一下。
变量名中不重复的有479个,这里面居然会有重名的变量!!
原来是因为有有一些变量忘了标记它来源于加速度传感器与三轴陀螺仪中的X轴,Y轴还是Z轴了,因此重复的变量名都是三个成对地出现,比如fBodyAcc-bandsEnergy()-1,8,出现了三次。
1
| which(cnames == "fBodyAcc-bandsEnergy()-1,8")
|
把-X,-Y,-Z补回去即可。前面提到要把-,()给去除掉,这里面用到一个小技巧,直接用把data.frame(samsungData),即可把变量名中的怪异字符改成.。
1 2 3 4 5 6 7 8 9 10 11 12
| cnames[303:344] = paste(cnames[303:344], rep(c("-X", "-Y", "-Z"), each = 14), sep = "") cnames[382:423] = paste(cnames[382:423], rep(c("-X", "-Y", "-Z"), each = 14), sep = "") cnames[461:502] = paste(cnames[461:502], rep(c("-X", "-Y", "-Z"), each = 14), sep = "") names(samsungData) = cnames samsungData = data.frame(samsungData) samsungData$activity = as.factor(samsungData$activity)
|
这个数据集当中不存在空值,并且看了它的说明,每个变量都已经做过标准化处理,全部是数值型变量,数值范围 [-1,1]。因此之后就不需要对变量做其他处理了。
1 2
| sum(is.na(samsungData))
|
数据集切分
把原始数据集分为training set和test set。课上规定说1、3、5、6号志愿者必须在training set中,27、28、29、30必须在test set中。因此剩下的subject,就平均分配给这两个set。
1 2 3 4 5 6 7
| totSubjects = unique(samsungData$subject) trainSubjects = c(1, 3, 5, 6) testSubjects = c(27, 28, 29, 30) remainSubjects = setdiff(setdiff(totSubjects, trainSubjects), testSubjects) set.seed(123) (trainSubjects = c(trainSubjects, sample(remainSubjects, ceiling(length(remainSubjects)/2))))
|
1
| ## [1] 1 3 5 6 14 22 15 21 25 7 26
|
1
| (testSubjects = c(testSubjects, setdiff(remainSubjects, trainSubjects)))
|
1
| ## [1] 27 28 29 30 8 11 16 17 19 23
|
1 2 3
| trainData = samsungData[samsungData$subject %in% trainSubjects, ] testData = samsungData[samsungData$subject %in% testSubjects, ]
|
建模
Classification and Regression Tree (C&RT)
这里直接把所有变量都拿去建模,让决策树自己去选择重要的变量。这里应该先尝试用PCA或者SVD降维一下会比较好, 但不想把过程搞的太复杂,因此降维这事情以后可以尝试一下。
1 2 3 4 5
| library(tree) par(mfrow = c(1, 1)) tree1 = tree(activity ~ ., data = trainData[, -562]) summary(tree1)
|
1 2 3 4 5 6 7 8 9 10 11
| ## ## Classification tree: ## tree(formula = activity ~ ., data = trainData[, -562]) ## Variables actually used in tree construction: ## [1] "fBodyAccJerk.bandsEnergy...1.16.X" "tGravityAcc.mean...X" ## [3] "tGravityAcc.max...Y" "tBodyAcc.max...X" ## [5] "tGravityAcc.arCoeff...Y.2" "tBodyAccMag.arCoeff..1" ## [7] "tGravityAcc.energy...Y" "fBodyAccMag.mad.." ## Number of terminal nodes: 9 ## Residual mean deviance: 0.496 = 1880 / 3800 ## Misclassification error rate: 0.0825 = 314 / 3804
|
C&RT最终挑选了8个变量。其中训练集的表现是错分率8.25%,测试集的表现是错分率14.43%。
1
| sum(testData$activity != predict(tree1, newdata = testData, type = "class"))/nrow(testData)
|
看看test set的confusion matrix。发现sitting和standing之间搞错的比较多,walk, walkdown, walkup之间错的也不少
1 2
| table(predict(tree1, newdata = testData, type = "class"), testData$activity)
|
1 2 3 4 5 6 7 8
| ## ## laying sitting standing walk walkdown walkup ## laying 699 15 0 0 0 0 ## sitting 0 528 139 0 0 0 ## standing 0 94 542 0 0 0 ## walk 0 0 0 472 35 59 ## walkdown 0 0 0 67 419 66 ## walkup 1 0 0 20 16 376
|
用10-fold cross-validation来测试一下树的内部节点个数定为多少比较合适,太少准确度低,太多容易overfitting。
1 2 3 4
| par(mfrow = c(1, 2)) plot(cv.tree(tree1, FUN = prune.tree, method = "misclass")) plot(cv.tree(tree1, FUN = prune.tree, method = "deviance"))
|
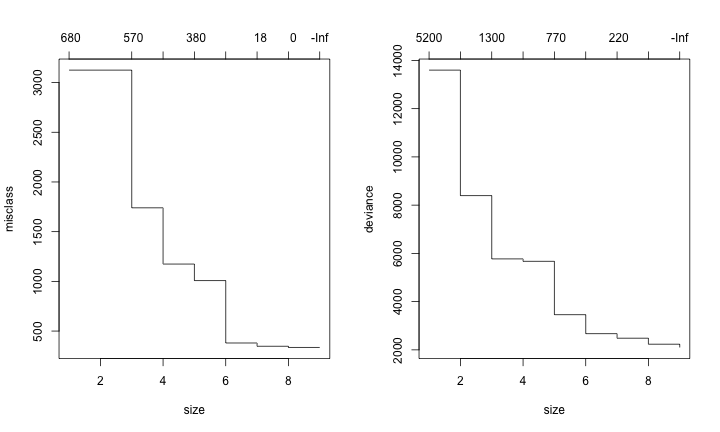
由上图可以看出,随着tree size的增大,错误率是在不断减少的,在内部节点数为8的时候最低,(又根据树的停止规则,它不会继续长超过8),因此内部节点数为8是比较好的选择。下面的code可以把这棵树画出来:
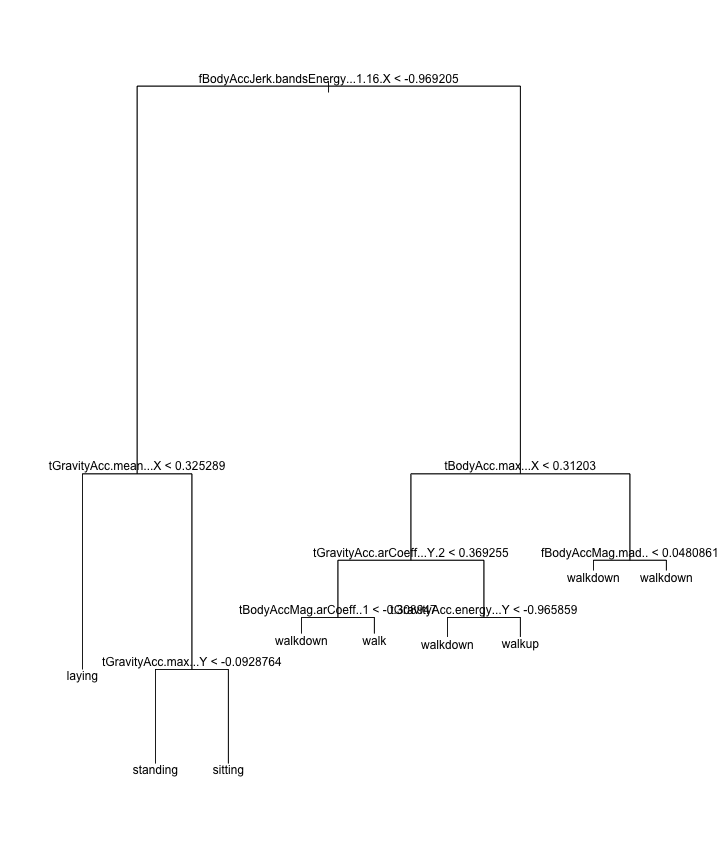
Random Forests 随机森林
关于随机森林的介绍,可以参考前一篇《林子大了,什么树都有》
1 2
| library(randomForest) rf1 = randomForest(activity ~ ., data = trainData[, -562])
|
1 2
| par(mfrow = c(1, 1)) varImpPlot(rf1, n.var = 10, main = "Random Forests: Top 10 Important Variables")
|
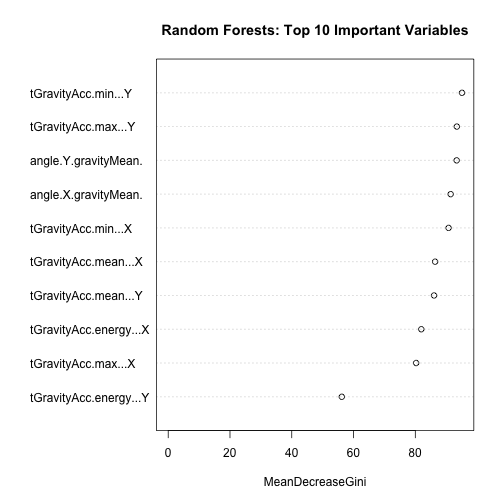
random forest中最重要的10个变量。
下面可以看到random forest在trainning set当中惊人的表现。1.31%的错分率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| ## ## Call: ## randomForest(formula = activity ~ ., data = trainData[, -562]) ## Type of random forest: classification ## Number of trees: 500 ## No. of variables tried at each split: 23 ## ## OOB estimate of error rate: 1.31% ## Confusion matrix: ## laying sitting standing walk walkdown walkup class.error ## laying 707 0 0 0 0 0 0.000000 ## sitting 0 634 14 0 0 1 0.023112 ## standing 0 18 675 0 0 0 0.025974 ## walk 0 0 0 662 2 3 0.007496 ## walkdown 0 0 0 2 509 5 0.013566 ## walkup 0 0 0 0 5 567 0.008741
|
再来看看test set的表现。8.37%的错分率,可见还是存在一点的overfitting,不过还好不算太严重。与之前单棵决策树相比,准确率高了不少。
1 2
| table(predict(rf1, newdata = testData), testData$activity)
|
1 2 3 4 5 6 7 8
| ## ## laying sitting standing walk walkdown walkup ## laying 700 15 0 0 0 0 ## sitting 0 538 132 0 0 0 ## standing 0 84 549 0 0 0 ## walk 0 0 0 534 2 17 ## walkdown 0 0 0 20 450 4 ## walkup 0 0 0 5 18 480
|
1 2
| sum(predict(rf1, newdata = testData) != testData$activity)/length(testData$activity)
|
总结
这次实验所用的数据是已经经过相关领域专家处理过的,并不是传感器采集到的raw data,这当中需要大量的相关知识,并且数据已经经过一定程度的标准化处理,因此不需要多做处理,分析难度大大降低。除此之外实验的目的是为了比较单一的决策树与随机森林这种ensemble的方法在分类准确度上的差异,因此没有费很大的功夫去想降维的方法。在实际应用中,降维是必须的,因为这种复杂的模型所需的计算量是比较大的,如果想在手机上进行预测,无法采用这么暴力的方法。除此之外,还可以尝试使用其他模型,譬如SVM,我用的是e1071这个r package,发现SVM的效果要比random forest要好一些,这里就不详述了。


