笔记整理自台大林轩田老师的开放课程-机器学习基石，笔记中所有图片来自于课堂讲义。

  上一篇比较深入地去理解了线性回归的思想和算法。分类和回归是机器学习中很重要的两大内容。而本篇要讲的Logistic Regression，名字上看是回归，但实际上却又和分类有关。

  之前提过的二元分类器如PLA，其目标函数为， $f(x)=sign(w^Tx)\in{-1,+1}$，输出要么是-1要么是+1，是一个“硬”的分类器。而Logistic Regression是一个“软”的分类器，它的输出是$y=+1$的概率，因此Logistic Regression的目标函数是 $\color{purple}{f}(x)=\color{orange}{P(+1|x)}\in [0,1]$。

方程的形式

$$h(x)=\frac{1}{1+exp(-w^Tx)}$$

  上面的方程背后有什么逻辑呢？

  假设医院知道一个病人的年龄、性别、血压、胆固醇水平，可以为他计算他得某种病的概率。最简单的做法就是对这几个特征进行加权求和：

$$\color{purple}{s}=\sum_{i=\color{red}{0}}^d\color{orange}{w_i}{x_i}=w^Tx$$

  但这里有个问题，就是 $\color{purple}{s}$ 的取值范围是$[-\infty,+\infty]$，而我们希望输出的是对该病人患病概率的一个估计，就需要把输出空间$[-\infty,+\infty]$转换到$[0,1]$上。如何变换？通过sigmoid函数 $\color{blue}{\theta}$ 。

$$\color{blue}{\theta}(\color{purple}{s})=\frac{e^\color{purple}{s}}{1+e^\color{purple}{s}}=\frac{1}{1+e^\color{purple}{-s}}$$

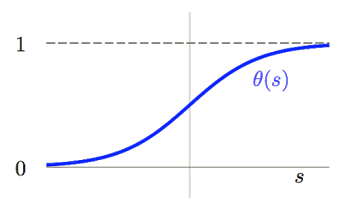
  因此，我们就可以利用经过sigmoid变换后的方程来对患病概率进行一个估计。

误差的衡量 - Cross Entropy Error

  有了方程的形式，我们就需要一个误差的衡量方式。上一篇我们讲到Linear Regression所使用的是平方误差，那么Logistic 可以使用平方误差吗？当然可以，error是人定的，你爱怎么定就怎么定，但是使用平方误差好不好，不好。为什么呢？

  如果使用平方误差，每个点产生的误差是：

$$\begin{aligned} err(h,x_n,y_n) &= \left\{ \begin{matrix} (\color{blue}{\theta}(w^Tx)-0)^2 & y_n=0 \\\ (1-\color{blue}{\theta}(w^Tx))^2 & y_n=1 \end{matrix}\right. \\\ &=y_n(1-\color{blue}{\theta}(w^Tx))^2+(1-y_n)\color{blue}{\theta}^2(w^Tx) \end{aligned}$$

  此时cost function，$E_{in}(w)=\sum{err}$就是一个关于$w$的非凸函数(non-convex)：

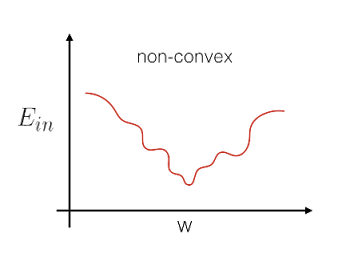
  非凸函数由于存在很多个局部最小点，因此很难去做最优化(解全局最小)。所以Logistic Regression没有使用平方误差来定义error，而是使用极大似然法来估计模型的参数。那么我们就要先来了解一下这个似然性(likelihood)。
  Logistic Regression的目标函数的输出是，在已知$x$的条件下，$y=+1$的概率，因此在已知$x$的条件下，$y=+1$的概率是$f(x)$，$y=-1$的概率是$1-f(x)$:

$$\color{purple}{f}(x)=\color{orange}{P(}\color{blue}{+1}\color{orange}{|x)} \Leftrightarrow \color{orange}{P(y|x)}= \left\{\begin{matrix} \color{purple}{f}\color{blue}{(x)} & \color{blue}{\text{for } y=+1}\\\ \color{red}{1-}\color{purple}{f}\color{red}{(x)} & \color{red}{\text{for }y=-1} \end{matrix}\right.$$

  考虑我们的训练样本$\mathcal{D}={(x_1,\color{blue}{+1}),(x_2,\color{red}{-1}),…,(x_N,\color{red}{-1})}$，并不是每次抽样都能抽到一模一样的$\mathcal{D}$，抽到这么一份样本是由于各种的机缘巧合。那么我们能抽到这么一份$\mathcal{D}$的概率取决于两部分：1、抽到样本$x_1,…,x_N$的概率；2、这些样本对应的$y_1,…,y_N$等于$\color{red}{+1}$的概率。

  对于目标函数 $\color{purple}{f}$，抽到$\mathcal{D}$的概率只取决于第1部分，而我们无法知道 $\color{purple}{f}$，即第2部分也是未知的，因此我们称在 $\color{orange}(h)$的作用下抽出$\mathcal{D}$的概率为“似然性”。如果 $\color{orange}{h}\approx\color{purple}{f}$，则 $likelihood(\color{orange}{h})\approx \text{probability using }\color{purple}{f}$，并且我们认为在 $\color{purple}{f}$的作用下，产生$\mathcal{D}$这样的样本的概率通常是非常的大的。

  所以有：

$$\text{if } \color{orange}{h}\approx\color{purple}{f}\text{, then }\; likelihood(\color{orange}{h})\approx(\text{probability using }\color{purple}{f})\approx\color{purple}{\text{large}}$$

  则理想的hypothesis就是能使得似然函数最大的那个$h$：
$$g=\underset{\color{orange}{h}}{argmax}\;likelihood(\color{orange}{h})$$

  当$\color{orange}{h}$是logistic函数的时候，即$h(x)=\theta(w^Tx)$，由于logistic函数的中心对称性，有:
$$1-h(x)=h(-x)$$

  所以有:

$$\begin{aligned} likelihood(\color{orange}{h})&=\color{grey}{P(x_1)}\color{orange}{h}\color{blue}{(x_1)}\color{grey}{\times P(x_2)}\color{red}{(1-\color{orange}{h}(x_2))}\color{grey}{\times ...\times P(x_N)}\color{red}{(1-\color{orange}{h}(x_N))} \\\ &= \color{grey}{P(x_1)}\color{orange}{h}\color{blue}{(x_1)}\color{grey}{\times P(x_2)}\color{red}{(\color{orange}{h}(-x_2))}\color{grey}{\times ...\times P(x_N)}\color{red}{(\color{orange}{h}(-x_N))} \\\ &= \color{grey}{P(x_1)}\color{orange}{h}\color{blue}{(x_1)}\color{grey}{\times P(x_2)}\color{red}{(\color{orange}{h}(y_2x_2))}\color{grey}{\times ...\times P(x_N)}\color{red}{(\color{orange}{h}(y_Nx_N))} \end{aligned}$$

  因此有这么一个相似性:

$$likelihood(logistic\;\color{orange}{h})\propto \prod_{n=1}^{N}\color{orange}{h}(y_nx_n)$$

  我们的目标是想找到一个似然性最大的方程:

$$\underset{\color{orange}{h}}{max}\;\;\color{grey}{likelihood(logistic\;\color{orange}{h}) \propto}\prod_{n=1}^{N}\color{orange}{h}(y_nx_n)$$

  转化成与参数$w$有关的形式:

$$\begin{aligned} \underset{\color{orange}{w}}{max}\;\;\color{grey}{likelihood(\color{orange}{w})} &\propto\prod_{n=1}^{N}\theta(y_n\color{orange}{w}^Tx_n) \\\ &\propto ln\prod_{n=1}^{N}\theta(y_n\color{orange}{w}^Tx_n) \\\ &\propto \color{grey}{\frac{1}{N}}\sum_{n=1}^{N}ln\,\theta(y_n\color{orange}{w}^Tx_n) \end{aligned}$$

  求解上式最大值，等价于求解下式的最小值:

$$\begin{aligned} &\;\;\;\;\underset{\color{orange}{w}}{min}\;\color{grey}{\frac{1}{N}}\sum_{n=1}^{N}-ln\,\theta(y_n\color{orange}{w}^Tx_n) \\\ &\Rightarrow \underset{\color{orange}{w}}{min}\;\color{grey}{\frac{1}{N}}\sum_{n=1}^{N}ln(1+exp(-y_n\color{orange}{w}^Tx_n)) \end{aligned}$$

  求和符号后面的部分就是在极大似然估计下，logistic方程的误差函数，这种形式的误差函数称为cross entropy error:

$$err(\color{orange}{w},x,y)=ln(1+exp(-y\color{orange}{w}x))\\
\color{blue}{\text{cross-entropy error}}$$

Cost function

  有了误差函数后，我们就可以定出Cost function:

$$E_{in}(\color{orange}{w})=\frac{1}{N}\sum_{n=1}^{N}ln(1+exp(-y_n\color{orange}{w}^Tx_n))$$

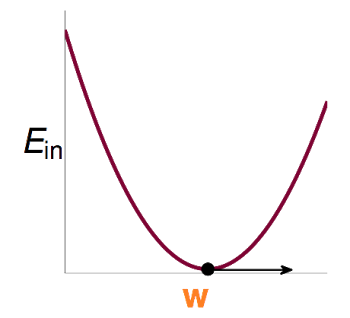
  该函数是连续，可微，并且是凸函数(二次微分矩阵是正定的)。

如何最小化$E_{in}(w)$

  那么如何能够最小化$E_{in}(w)$呢？按照之前Linear Regression的逻辑，由于它是凸函数，如果我们能解出一阶微分(梯度)为0的点，这个问题就解决了。

  先来看看$E_{in}(w)$在$w_i$方向上的偏微分：

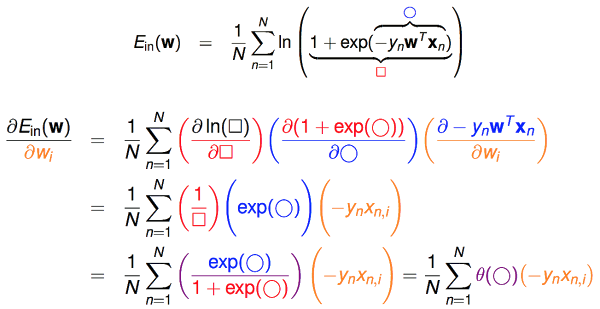
  再把偏微分方程中的$x_{n,i}$换成向量的形式，就得到$E_{in}(w)$的一阶微分:

$$\triangledown E_{in}(w)=\frac{1}{N}\sum_{n=1}^{N}\color{purple}{\theta(\color{black}{-y_nw^Tx_n})}\color{orange}{(-y_nx_n)}$$

  和之前的Linear Regression不同，它不是一个线性的式子，要求解$\triangledown E_{in}(w)=0$这个式子，是困难的。那么该使用何种方法实现$E_{in}(w)$最小化呢？

  这里可以使用类似PLA当中的，通过迭代的方式来求解，这种方法又称为梯度下降法(Gradient Descent)。

  For t = 0, 1, …
$$w_{t+1} \leftarrow w_t + \color{red}{\eta}\color{blue}{v}$$
  when stop, return $\color{purple}{\text{last w as g}}$

  其中$\color{red}{\eta}$为每步更新的大小(step size)，$\color{blue}{v}$是单位向量，表示每次更新的方向。

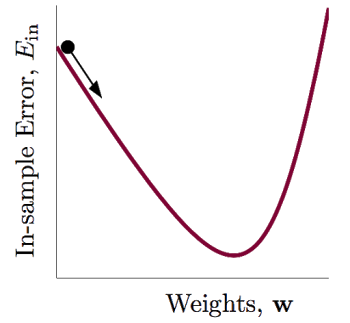
  有点类似一个小球，往山谷方向滚，直至山谷。每一步我们只要决定两个东西：1、滚动的方向；2、滚动的步长。

  滚动的方向好决定，即在该点一阶微分后的向量所指的方向：

$$\color{blue}{v}=-\frac{\triangledown E_{in}(w_t)}{||\triangledown E_{in}(w_t)||}$$

  步长 $\color{red}{\eta}$比较难决定，太小了，更新太慢，太大了，容易矫枉过正:

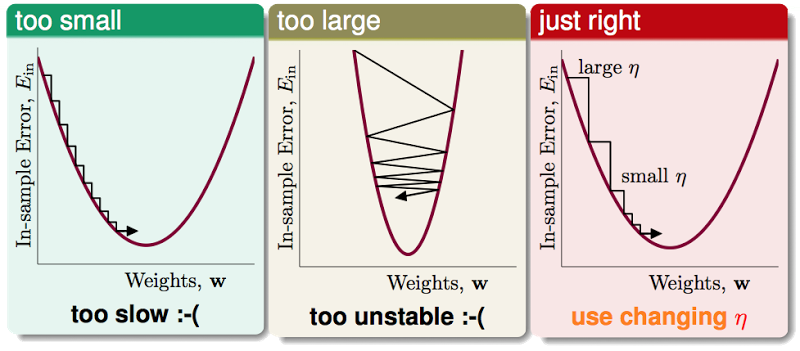
  一个比较好的做法是让 $\color{red}{\eta}$ 与 $\color{blue}{||\triangledown E_{in}(w_t)||}$ 成一定的比例，让新的和$\color{blue}{||\triangledown E_{in}(w_t)||}$成比例的$\color{purple}{\text{紫色的 }\eta}$ 来代替原来$\color{red}{\text{红色的 }\eta}$：

$$\begin{aligned} w_{t+1} \leftarrow & w_t - \color{red}{\eta} \color{blue}{\frac{\triangledown E_{in}(w_t)}{||\triangledown E_{in}(w_t)||}} \\\ &\;\;\;\;\;\;\;\;\;\parallel \\\ &w_t - \color{purple}{\eta}\,\color{blue}{\triangledown E_{in}(w_t)} \end{aligned}$$

  我们称这个$\color{purple}{\text{紫色的 }\eta}$ 为 $\color{purple}{\text{fixed learning rate}}$。

  再来完整的梳理下梯度下降法(Gradient Descent):

  initialize $w_0$

  For t = 0, 1, …

  1. compute

$$\triangledown E_{in}(w)=\frac{1}{N}\sum_{n=1}^{N}\color{purple}{\theta(\color{black}{-y_nw^Tx_n})}\color{orange}{(-y_nx_n)}$$

  2. update by

$$w_t - \color{purple}{\eta}\,\color{blue}{\triangledown E_{in}(w_t)}$$

  …until $\color{orange}{E_{in}(w_{t+1})=0}$ or enough iterations

  return $\color{purple}{\text{last }w_{t+1}\text{ as }g}$