笔记整理自台大林轩田老师的开放课程-机器学习基石，笔记中所有图片来自于课堂讲义。

  上一篇用成长函数$m_{\mathcal{H}}(N)$来衡量Hypotheses Set $\mathcal{H}$中有效的方程的数量(Effective Number of Hypotheses)，以取代Hoeffding’s Inequality中的大$M$，并用一种间接的方式 —- break point，来寻找$m_{\mathcal{H}}(N)$的上界，从而避免了直接研究$\mathcal{H}$的成长函数的困难。

学习所需”维他命”(The VC Dimension)

$$m_{\mathcal{H}}(N)\leq \sum_{i=0}^{k-1}\binom {N}{i}$$
  根据之前得到的式子，我们知道如果一个$\mathcal{H}$存在break point，我们就有办法保证学出来的东西能够“举一反三”(good generalization)。一般来说break point越大的$\mathcal{H}$，其复杂度也更高，我们可以使用vc dimension来描述一个$\mathcal{H}$的复杂程度，这个vc dimension来自Vladimir Vapnik与Alexey Chervonenkis所提出的VC Theory。

  根据定义，一个$\mathcal{H}$的vc dimension(记为$d_{vc}(\mathcal{H})$)，是这个$\mathcal{H}$最多能够shatter掉的点的数量 (the largest value of N for which $m_{\mathcal{H}}(N)=2^N$)，如果不管多少个点$\mathcal{H}$都能够shatter他们，则$d_{vc}(H)=\infty$。不难看出$d_{vc}$与break point k的关系，有$k=d_{vc}+1$，因此我们用这个$d_{vc}$来描述成长函数的上界：
$$m_{\mathcal{H}}(N)\leq \sum_{i=0}^{d_{vc}} \binom {N}{i}$$
  上式右边(RHS)事实上是最高项为$d_{vc}$的多项式，利用数学归纳法可得：
$$m_{\mathcal{H}}(N)\leq \sum_{i=0}^{d_{vc}} \binom {N}{i} \leq N^{d_{vc}}+1$$

更加一般化的Bound (The VC Generalization Bound)

  上一篇的末尾我们设想利用有限的$m_{\mathcal{H}}(N)$来替换无限的大$M$，得到$\mathcal{H}$遇到Bad Sample的概率上界：
$$\mathbb{P}_\mathcal{D}[BAD\ D]\leq 2m_{\mathcal{H}}(N)\cdot exp(-2\epsilon ^2N)$$
  其中$\mathbb{P}_\mathcal{D}[BAD\ D]$是$\mathcal{H}$中所有有效的方程(Effective Hypotheses)遇到Bad Sample的联合概率，即$\mathcal{H}$中存在一个方程遇上bad sample，则说$\mathcal{H}$遇上bad sample。用更加精准的数学符号来表示上面的不等式：
$$\mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon]\leq 2m_{\mathcal{H}}(N)\cdot exp(-2\epsilon ^2N)$$
  注：$\exists h \in \mathcal{H}\text{ s.t. }$ - $\mathcal{H}$中存在($\exists$)满足($\text{ s.t }$)…的$h$

  但事实上上面的不等式是不严谨的，为什么呢？$m_{\mathcal{H}}(N)$描述的是$\mathcal{H}$作用于数据量为$N$的资料$\mathcal{D}$，有效的方程数，因此$\mathcal{H}$当中每一个$h$作用于$\mathcal{D}$都能算出一个$E_{in}$来，一共能有$m_{\mathcal{H}}(N)$个不同的$E_{in}$，是一个有限的数。但在out of sample的世界里(总体)，往往存在无限多个点，平面中任意一条直线，随便转一转动一动，就能产生一个不同的$E_out$来。$E_{in}$的可能取值是有限个的，而$E_{out}$的可能取值是无限的，无法直接套用union bound，我们得先把上面那个无限多种可能的$E_{out}$换掉。那么如何把$E_{out}$变成有限个呢？
  假设我们能从总体当中再获得一份$N$笔的验证资料(verification set)$\mathcal{D}’$，对于任何一个$h$我们可以算出它作用于$\mathcal{D}’$上的$E_{in}^{‘}$，由于$\mathcal{D}’$也是总体的一个样本，因此如果$E_{in}$和$E_{out}$离很远，有非常大的可能$E_{in}$和$E_{in}^{‘}$也会离得比较远。

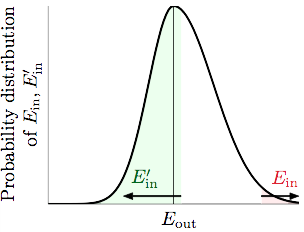
  事实上当N很大的时候，$E_{in}$和$E_{in}^{‘}$可以看做服从以$E_{out}$为中心的近似正态分布(Gaussian)，如上图。$[|E_{in}-E_{out}|\text{ is large}]$这个事件取决于$\mathcal{D}$，如果$[|E_{in}-E_{out}|\text{ is large}]$，则如果我们从总体中再抽一份$\mathcal{D}^{‘}$出来，有50%左右的可能性会发生$[|E_{in}-E_{in}^{‘}|\text{ is large}]$，还有大约50%的可能$[|E_{in}-E_{in}^{‘}|\text{ is not large}]$。
  因此，我们可以得到$\mathbb{P}[|E_{in}-E_{out}|\text{ is large}]$的一个大概的上界可以是$2\mathbb{P}[|E_{in}-E_{in}^{‘}|\text{ is large}]$，以此为启发去寻找二者之间的关系。

  引理：

$$(1-2e^{-\frac{1}{2}\epsilon^2N})\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]\leq \mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{‘}(h)| \gt \frac{\epsilon}{2}]$$

  上面的不等式是从何而来的呢？我们先从RHS出发：

$$\begin{aligned} &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &\geq \mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2} \mathbf{\;and\;} \underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &=\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \;\times \\\ &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\;\;\;\,\text{(注：sup - 上确界，最小上界。)} \end{aligned}$$

  上式第二行的不等号可以由$\mathbb{P}[\mathcal{B}_1]\geq \mathbb{P}[\mathcal{B}_1 \textbf{ and } \mathcal{B}_2]$得到，第三、四行则是贝叶斯公式，联合概率等于先验概率与条件概率之积。

  下面来看看不等式的最后一项$\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{‘}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]$。对于一个固定的data set $\mathcal{D}$来说，我们任选一个$h^{*}$使得$|E_{in}(h^{*})-E_{out}(h^{*})|\gt \epsilon$，注意到这个$h^{*}$只依赖于$\mathcal{D}$而不依赖于$\mathcal{D}^{‘}$噢，对于$\mathcal{D}^{‘}$来说可以认为这个$h^{*}$ is forced to pick out。

  由于$h^{*}$是对于$\mathcal{D}$来说满足$|E_{in}-E_{out}|\gt \epsilon$的任意一个hypothesis，因此可以把式子中的上确界(sup)先去掉。

$$\begin{aligned} &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\geq \mathbb{P}[|E_{in}(h^{*})-E_{in}^{'}(h^{*})| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \end{aligned}$$

  这里就要稍微出动一下前人的智慧了：

$$\left.\begin{matrix} |E_{in}^{'} - E_{out}|\leq \frac{\epsilon}{2}\\\ |E_{in}-E_{out}| \gt \epsilon \end{matrix}\right\} \Rightarrow |E_{in}-E_{in}^{'}| \gt \frac{\epsilon}{2}$$

  为了直观一点$h^{*}$就不写了。经过各种去掉绝对值符号又加上绝对值符号的运算，可以发现LHS的两个不等式是RHS那个不等式的充分非必要条件。而LHS第二个不等式是已知的，对于$h^{*}$必成立的。因此我们拿LHS这个充分非必要条件去替换RHS这个不等式，继续前面的不等式：

$$\begin{aligned} &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\geq \mathbb{P}[|E_{in}(h^{*})-E_{in}^{'}(h^{*})| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\geq \mathbb{P}[|E_{in}^{'}(h^{*})-E_{out}(h^{*})| \leq \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\geq 1-2e^{-\frac{1}{2}\epsilon^2N} \end{aligned}$$

  最后一个不等号动用了Hoeffding Inequality：

$$\begin{aligned} &\;\;\;\,\mathbb{P}[|...|\gt \epsilon]\leq 2Mexp(-2\epsilon^2N) \\\ &\Leftrightarrow 1-\mathbb{P}[|...|\gt \epsilon]\geq 1-2Mexp(-2\epsilon^2N) \\\ &\Leftrightarrow \mathbb{P}[|...|\leq \epsilon]\geq 1-2Mexp(-2\epsilon^2N) \end{aligned}$$

  之前说过对于$\mathcal{D}^{‘}$来说，$h^{*}$ is forced to pick out，因此$M=1$。接着把$\epsilon$替换为$\frac{\epsilon}{2}$，就成了$\mathbb{P}[|…|\lt \frac{\epsilon}{2}]\geq 2exp(-\frac{1}{2}\epsilon^2N)$。则我们可以得到引理中的不等式。

  对于$e^{-\frac{1}{2}e^2N}$，一个比较合理的要求是$e^{-\frac{1}{2}\epsilon^2N}\lt \frac{1}{4}$，譬如我们有400笔资料，想要$E_{in}$和$E_{out}$相差不超过0.1。注意到这只是一个bound，只要要求不太过分，也不能太宽松即可，适当的宽松一点是OK的。当然这里也是想跟之前所说的 “$\mathbb{P}[|E_{in}-E_{out}|\text{ is large}]$的一个大概的上界可以是$2\mathbb{P}[|E_{in}-E_{in}^{‘}|\text{ is large}]$” 当中的2倍有所结合。

  所以就有$1-2e^{-\frac{1}{2}e^2N}\gt \frac{1}{2}$。带回引理，可得：

$$\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]\leq 2\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{‘}(h)| \gt \frac{\epsilon}{2}]$$

  这样一来我们就把无限多种的$E_{out}$换成了有限多种的$E_{in}$，因为$\mathcal{D}$与$\mathcal{D}^{‘}$的大小相等，都为$N$，因此我们手中一共有$2N$笔数据，这样$\mathcal{H}$作用于$\mathcal{D}+\mathcal{D}^{‘}$最多能产生$m_{\mathcal{H}}(2N)$种dichotomies。此时我们针对上面的不等式，就又可以使用union bound了。(关于union bound，可以参考上一篇VC Dimension, Part I)

$$\begin{aligned} \mathbb{P}[BAD] &\leq 2\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &\leq 2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &\text{(用固定的hypothesis去看$E_{in}$与$E_{in}^{'}$的差别。)} \end{aligned}$$

  前面的动作相当于先从总体中抽出$2N$笔数据，把这$2N$笔数据当成一个比较小的bin，然后在这个bin中抽取$N$笔作为$\mathcal{D}$，剩下的$N$笔作为$\mathcal{D}^{‘}$，$\mathcal{D}$和$\mathcal{D}^{‘}$之间是没有交集的。在我们想象出来的这个small bin当中，整个bin的错误率为$\frac{E_{in}+E_{out}}{2}$，又因为：

$$|E_{in}-E_{in}^{‘}|\gt \frac{\epsilon}{2} \Leftrightarrow |E_{in} - \frac{E_{in}+E_{in}^{‘}}{2}|\gt \frac{\epsilon}{4}$$

  所以用RHS替换LHS之后，前面不等式就又可以使用Hoeffding inequality了：

$$\begin{aligned} \mathbb{P}[BAD] &\leq 2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &=2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-\frac{E_{in}(h)+E_{in}^{'}(h)}{2}| \gt \frac{\epsilon}{4}]\\\ &\;\;\;\text{(Hoeffding without replacement)} \\\ &\leq 2\,m_{\mathcal{H}}(2N)\cdot 2\,exp(-2(\frac{\epsilon}{4})^2N) \end{aligned}$$

  这上面千辛万苦得出来的这个bound就叫做Vapnik-Chervonenkis (VC) bound：

$$\begin{aligned} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \end{aligned}$$